Forum de Mathématiques: Maths-Forum

En effet, il faut résoudre sin(3x+Pi/6)=sin(0)
J'utilise alors 3x+Pi/6=0+2*k*Pi et 3x+Pi/6=Pi-0+2*k*Pi k appartenant à Z

Bonjour,

Je ne sais pas comment résoudre :

sin(3x+Pi/6)=0 sur l'intervalle [0;2Pi]

Merci pour votre aide !

Oui c'est ce que je ferais Donc PRC ne fais pas attention à ce que j'ai écris c'était une grave erreur. Dérive ta fonction, et une fois fait tu étudies la continuité de cette dérivée. Je ne pense pas qu'il est nécessaire de la dériver car dans mon exercice, on me demande de la dériver à la prochain...

tan(t) = sin(t)/cos(t) Donc tu as cos(t) qui est en dénominateur à 2 reprises sur cette fonction. Donc quand est-ce que la fonction pourrait admettre une limite (donc ne pas être continue) ? Quand les dénominateur sont égaux à 0, donc quand cos(t) vaut 0. Et donc, ta fonction est dérivable sur [0;P...

Bonsoir,

Je n'arrive pas à justifier la dérivabilité de sur [0;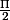[ :mur: ...

Quelqu'un pourrait-il me donner une piste :id: ... ?

Merci :we: !

Ok, merci ! Donc je fais comme si n était un entier "Démontrer que (1+a)^n>=1+na avec a E R+* Par résurrence... (Pn) "(1+a)^n>=1+na Initialisation (P0) : "(1+a)^0>=1+0*a" On a 1>= 1 Donc (P0) est vraie" Hérédité Soit k un entier fixé, Supposons que (Pk) soit vraie, Alors (1+a)^k>=1+ka Montrons que l...

Bonsoir,

"Démontrer que (1+a)^n>=1+na avec a E R+*

Par résurrence...

(Pn) "(1+a)^n>=1+na

Initialisation
(P0) : "(1+a)^0>=1+0*a
On a 1>= 1
Donc (P0) est vraie"

Ici n n'est pas forcément un entier naturel ?

J'essaierai de le montrer ultérieurement car je n'ai plus le temps...
J'ai donc remplacé 1+2+...+n par n(n+1)/2, j'ai développé et simplifié et je me retrouve donc avec (1+2+...+k+(k+1))²=1^3+2^3+k^3+(k+1)^3 !
Merci beaucoup !!!!!!!

Ok, tout ce qu'il reste à montrer, c'est que 2(k+1)(1+2+...+k)+(k+1)² = (k+1)^3. Tu es d'accord avec ça?

Tout à fait d'accord.

Je te laisse alors essayer de le montrer. Au passage, connais-tu une expression simple de 1+2+...+k ? Elle pourrait nous aider.

Non...

J'ai donc
(1+2+...+k+(k+1)² = (1^3+2^3+...+k^3)+(k+1)(2*(1+2+...+k)+(k+1))
Mais la...

Pour ça, je te propose de développer (1+2+...+(k+1))² en utilisant l'identité remarquable (a+b)²=a²+2ab+b² en prenant a=1+2+...+k et b=k+1

Je n'y avait pas pensé ! Je m'y remets de suite... !

Je ne vois pas quoi faire à part développer (1+2+...+k+(k+1))^2 qui, je pense, n'est pas la bonne solution... !

Je pars de ça : (1+2+...+k)^2=1^3+2^3+...+k^3
Ou de ça plutôt (1+2+...+k+(k+1))^2 ?

Par contre, au moment de l'hérédité j'écris :
Soit k un entier fixé,
Supposons que (Pk) soit vraie,
Donc ...............
Je ne sais pas comment l'écrire ici...

Ah oui, je partais mal déjà...
Pour n=1 on a bien 1^3=1^2=1
Pour n=2 on a bien 1^3+2^3=(1+2)^2=9
Je recommence tout alors...

De quelle manière puis-je calculer la propriété au rang initial ?
Ce sont les pointillés qui me bloquent...

Je me doute qu'il faut faire par récurrence (c'est un exercice d'application du raisonnement par récurrence) mais je ne sais pas comment m'y prendre...

Bonsoir,

Je n'arrive pas à démontrer cette égalité :
1^3+2^3+...+n^3 = (1+2+3+...+n)^2

Merci pour votre aide !

Comment puis-je trouver n0 maintenant ?

On aurait alors tn E ]1/3-10^-2;1/3+10^-2[ ?