Forum de Mathématiques: Maths-Forum

Je ne connais pas cette methode :S

Bonjour pouvez vous m'aider avec le calcul de l'inverse de cette matrice :





Merci !

En effet, merci !


Pour la question 3, suffit-il de montrer que A est inversible pour en déduire que est bijective?

Bonjour, pouvez-vous m'aider avec cet exercice? Soit E = {f:R \rightarrow R | \exists (a,b,c,d) \in R^4, \forall x \in R,f(x)= ae^-^x.cos(x)+be^-^x.sin(x) + cxe^{-x}.cos(x) + dxe^{-x}.sin(x) } On pose f_1(x)= e^-^xcos(x) , f_2(x)...

excusez moi mais je ne comprends pas ce resultat

Bonjour soit la suite telle que :





je dois etudier son sens de variation mais je ne sais pas comment calculer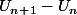




Merci !

c'est effectivement ce que j'ai fait mais je ne sais pas etudier le signe du denominateur

je viens de voir comment montrer qu'elle est majorée mais je ne sais pas quoi faire pour le sens de variation

titine a écrit:Ce n'est pas un problème !

As tu vu les démonstrations par récurrence ?

oui je les ai vues

Bonjour, pouvez vous m'aider ? (Un) est la suite définie par : U_0=0 et pour tout entier n, U_n_+_1=\sqrt{U_n+6} 1) Calculez U_1,U_2 et U_3 j'ai un probleme car je tombe sur racine de racine de racine ... 2) Prouvez que la suite (Un) est croissante et majorée par 3. Que pouvez vous en déduire? je ne...

Judoboy a écrit:Bon bah je crois que c'est fini

merci beaucoup vraiment!

Judoboy a écrit:Oui, parce que ?

l'integrale de x^n donne 1/(n+1) qui tend vers 0 et In est superieure a 0 donc d'après le theoreme des gendarmes..

Judoboy a écrit:Oulah non, x varie entre 0 et 1, il va plutôt se passer l'inverse.

Calcule l'intégrale de 0 à 1 de x^n, et sers-toi des propriétés que tu connais sur les intégrales.

Si je ne me suis pas trompée la limite de est 0 non?

Judoboy a écrit:ln(1+y) 0, et quelque soit y > 0 il existe x > 0 tel que y = x^n.

Tu as donc ln(1+x^n) < x^n.

Pour la 3 tu encadres In.

d'accord merci beaucoup! et pour la limite de x^n je peux dire que c'est + l'infini en +l'infini directement ?

Judoboy a écrit:Pour la 2, tu as ln(1+x) 0, c'est vrai en particulier pour x^n.

comment expliquer que c'est vrai pour x^n ?

Manny06 a écrit:je t'ai déjà donné des indications
à quel endroit bloques-tu ?

Pardon je me suis mal exprimée. J'ai pu trouvée qu'elle etait decroissante grace a votre indication. Je voulais savoir si vous pouviez maintenant m'aider avec les 2 autres questions ?

Manny06 a écrit:NON
x^(n+1)=(x^n)*x

effectivement, je viens de comprendre mon erreur, merci! Pouvez vous m'aider pour la suite ?

Manny06 a écrit:sur [0;1] compare x^n et x^(n+1)

tu en deduiras facilement la monotonie de In (mais je pense qu'elle est décroissante et minorée)
si tu as étudié les variations de g tu as du trouver qu'elle était decroissante à partir de 0 donc négative

Je crois que j'ai trouvé a condition que x^n.x^n = x^(n+1)

Bonjour, On a I_n=\int_0^{1} ln(1+x^n) dx Il faut etudier les varations de cette suite . Je sais qu'il faut faire I_{n+1}-I_n mais je n'arrive pas a aboutir a un resultat en calculant. on trouve qu'elle est croissante et d'après les questions précedentes on en déduit qu'elle est convergente....

aidez moi svp ! :(