18 résultats trouvés
Revenir à la recherche avancée
Ah oui, j'ai oublié de répondre,
le prof a donné la correction, cétait correcte et le 3 cétait bien un arc de cercle
- par GFX
- 08 Déc 2011, 19:46
-
- Forum: ✎✎ Lycée
- Sujet: Limite
- Réponses: 13
- Vues: 656
el niala a écrit:OK pour ton résultat
et pourquoi utiliser hopital en dernier recours ? parfois ça va vite
et parfois on se plante aussi :zen:
ok merci

- par GFX
- 08 Déc 2011, 19:20
-
- Forum: ✎✎ Lycée
- Sujet: Limite
- Réponses: 13
- Vues: 656
non, ce n'est pas ce que j'ai écrit ! je t'ai écrit que la règle de Lhospital était à utiliser en dernier recours (ton professeur a dû vous le dire) et que généralement la limite en l'infini de ln(x)/x (qui vaut 0) se traouvait en étudiant g(x)=\sqrt{x}-\ln x comme tu connais cette limite e...
- par GFX
- 08 Déc 2011, 18:56
-
- Forum: ✎✎ Lycée
- Sujet: Limite
- Réponses: 13
- Vues: 656
pourquoi et comment trouver la

en faisant celle de
)
- par GFX
- 08 Déc 2011, 18:41
-
- Forum: ✎✎ Lycée
- Sujet: Limite
- Réponses: 13
- Vues: 656
el niala a écrit:as-tu au préalable établi que :

?
Oui avec la règle de L'Hôpital

- par GFX
- 08 Déc 2011, 17:51
-
- Forum: ✎✎ Lycée
- Sujet: Limite
- Réponses: 13
- Vues: 656
Bonjour, comment calculer

car ça nous donne une FI :
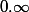
- par GFX
- 08 Déc 2011, 15:53
-
- Forum: ✎✎ Lycée
- Sujet: Limite
- Réponses: 13
- Vues: 656
http://djr9.olympe-network.com/ExMath98.jpg Quelqu'un peut il me dire si mes réponses son juste ? 1) \frac{\pi H^3}{2} 2) \frac{\pi H^3}{6} 3) ? 4) \frac{\pi H^2}{4} 5) \frac{\pi H^5}{10} Pour le 3 je ne sais pas qu'elle fonction c'est, ((e^x+e^-x)/2)-1 ? Merci
- par GFX
- 07 Déc 2011, 16:14
-
- Forum: ✎✎ Lycée
- Sujet: Exercice : calcul de volum [Integrale]
- Réponses: 1
- Vues: 379
L'énoncé de départ c'est
 dx)
J'ai fait par partie en disant que f = x et g = cos(x²+9)
- par GFX
- 23 Nov 2011, 16:49
-
- Forum: ✎✎ Lycée
- Sujet: Primitivation
- Réponses: 4
- Vues: 563
Bonjour,
Comment doit on procéder pour faire la primitive de
 dx)
?
Il doit certainement avoir
)
mais comment faire tomber le 2x
mais je n'arrive pas, quelqu'un pourrait-il m'aider ?
- par GFX
- 23 Nov 2011, 16:12
-
- Forum: ✎✎ Lycée
- Sujet: Primitivation
- Réponses: 4
- Vues: 563
Black Jack a écrit:Attention que le changement de variable n'est pas, je pense, au programme en Secondaire.
:zen:
Si mais je n'etais pas la quand le prof a expliqué
- par GFX
- 21 Nov 2011, 17:26
-
- Forum: ✎✎ Lycée
- Sujet: Primitive
- Réponses: 10
- Vues: 691
Merci beaucoup, je comprend mieux
ce qui donne donc
^3}{7}+\dfrac{3(x-1)^2}{3}+\dfrac{3(x-1)}{3}+1))
- par GFX
- 21 Nov 2011, 17:00
-
- Forum: ✎✎ Lycée
- Sujet: Primitive
- Réponses: 10
- Vues: 691
fibonacci a écrit:Bonsoir;
on pose


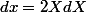
la primitive devient
^3}{X}\times2XdX)
Merci mais
Je comprend jusque

Aprés je ne comprend plus
- par GFX
- 19 Nov 2011, 19:11
-
- Forum: ✎✎ Lycée
- Sujet: Primitive
- Réponses: 10
- Vues: 691
Bonsoir, Je n'arrive pas a faire la primitive de \dfrac{x^3}{sqrt{x-1}} J'essaye de faire quelque chose comme ce-ci \int x^3.(x-1)^{-1/2} = \dfrac{3x^2.sqrt{(x-1)^3}}{3/2} - \int \dfrac{6x.sqrt{(x-1)^3}}{3/2} Mais c'est surement pas comme ça que l'on doit faire. Merci pour vo...
- par GFX
- 19 Nov 2011, 17:55
-
- Forum: ✎✎ Lycée
- Sujet: Primitive
- Réponses: 10
- Vues: 691
Ah merci beaucoup, je ne savais pas que ça existait une branche parabolique.
- par GFX
- 27 Oct 2011, 19:59
-
- Forum: ✎✎ Lycée
- Sujet: x/ln(x)
- Réponses: 5
- Vues: 1693
Bonsoir, quel est ton problème ? Pour la limite de x/ln(x) en l'infini la règle de l'hopital va donner la solution (et c'est aussi une limite connue normalement - ou ça le sera -). Ensuite ici ton problème ressemble à déterminer la limite en l'infini de 1/ln(x). Il n'y a surtout pas besoin de l'Hop...
- par GFX
- 27 Oct 2011, 18:41
-
- Forum: ✎✎ Lycée
- Sujet: x/ln(x)
- Réponses: 5
- Vues: 1693
Bonsoir,
Je n'arrive pas a calculer l'AO de x/ln(x)
je trouve
}}{x} = 0)
j'aplique le thérome de l'hopital
je dérive x/ln(x)
et au finale je trouve
} - \frac{1}{ln(x)^2} = 0)
comment faire ?
- par GFX
- 27 Oct 2011, 18:35
-
- Forum: ✎✎ Lycée
- Sujet: x/ln(x)
- Réponses: 5
- Vues: 1693