Forum de Mathématiques: Maths-Forum

pour a=b Les point M et N sont donc confondus. Et donc appartiennent à d. Ainsi M et N sont symétriques à d. pour a=-b a \ge b I le milieu [MN] est confondu a O ( du repère) M et N appartiennent donc a d':y=-x . la droite d' est perpendiculaire a d:y=x donc [MN] est perpendiculaire a d. Ainsi M...

el niala a écrit:considère le triangle MON,

pour que d - ie (OI) - soit axe de symétrie pour [MN], le fait que ce soit une médiane suffit-il ?

J'ai trouver pour les symétriques ! je te montre sa

Je ne comprend pas l'utilite de la 1)a

Ah si ! je crois comprendre mais cela veut dire qu'on admet que C' et C sont symétriques ..?

ne multiplie pas les posts, sinon, ça va vite devenir capharnaum ! pour 1c) tu as montré que le milieu de M(a,b) et N(b,a) était sur d, et tu conclus (abusivement) que N est le symétrique de M par rapport à d il existe une infinité de droites qui passent par I, pour autant il n'y en a qu'une qui es...

:stupid_in 2) c Réciproquement, soit N un point de C' . Démontrer que son symétrique N' par rapport à d appartient à C. On a C':y=x^2 et a>=0 Soit N(a;a^2) xN=a=yN' yN=a^2=xN' pour que N' soit le symétrique de N par rapport d y=x^2 a^2=(a)2 Je suis un peu "paumé...

Je suis un peu pommé ça, je ne sais pas, "paumé" peut-être un peu si tu poses N(a²,a) tu ne risques pas d'y arriver :triste: essaie plutôt N(a,a²) d'où son symétrique N'(a²,a) et tu devrais pouvoir conclure... Ah oui ! Mais pour le le 1)c je n'ai pas compris ce que je devais faire enfaite...

1c) non, ta démonstration est incomplète, ce n'est pas parce le milieu d'un segment est sur un droite que ses extrémités sont symétriques par rapport à cette droite, tu as oublié d'utiliser 1a) 2a) OK détail : pour \ge tape \ge (pour greater or equal) 2b) c'est un peu maladroit je trouve, explique ...

:stupid_in 2) c Réciproquement, soit N un point de C' . Démontrer que son symétrique N' par rapport à d appartient à C. On a C':y=x^2 et a>=0 Soit N(a^2;a) xN=a^2=yN' yN=a=xN' pour que N' soit le symétrique de N par rapport d y=sqrt(x) a=sqrt(a^2) Je suis un p...

2) b Démontrez que son symétrique M' par rapport à d appartient a C' On a M(a;sqrt(a)) et a>=0 et C':y=x^2 pour que M' soit le symétrique de M : xM=a=yM' xM'=sqrt(a)=yM et on a y=x^2 a=(sqrt(a)^2 Donc M'(sqrt(a);a)

c) En déduire que M et N sont symétriques par rapport à d Comme : xA=a=yB yA=b=xB I appartient à d alors A est symétrique à B par rapport à d. 2) Soit M le point d'abscisse a de C avec (a>=0) 2)a Quelles sont les coordonnées de M? Comme y=sqrt(x) et a>=0 alors le point M d'abscisse &...

1b) on a

I milieu de [MN] :

= =
= =


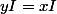donc I appartient à d :we:

ce n'est pas très lisible :doh: 1a) ça a l'air correct 1b) pas clair du tout, le milieu d'un segment a pour coordonnées la demi-somme des coordonnées des extrémités du segment, d'où celles de I, ne remarques-tu pas x_I=y_I par hasard ? Je crois avoir trouvé, j'envoie ce que j'ai trouvé :) PS : effe...

On considère la courbe ;) d'équation y=;)x et la courbe ;)' d'équation y=x² sur[0;+;)[. La droite d a pour équation y=x. 1 Soit les points M(a;b) et N(b;a) où a et b sont deux réels. a. Démontrer que OM=ON. [CENTER]Pour a et b ;)0 OM= ;)((a-0)²+(b-0)²)=;)((a²+b²) ON= ;)((b-0)²+(a-0)²)=;)((b²+a²) ;)(...

Einstein0883 a écrit:Bah... 1/x = 2x-1 2x^2 - x -1 =0 ce qui te donne je crois x = 1 ou x = 1/2 :lol3:

J'ai fais sa aussi mais j'ai du me planter dans le calcul au milieu "erreur de signe" Merci en tout cas ! ( je suis con ) x)

Je l'ai fais cela mais je trouve pas les deux point d'intersection. Un hyperbole et une fonction affine ont deux point d'intersection non?


(l'équation premier truc que j'ai fait au passage ;) ) mais bon je vous l'avait pas dit aussi !

Voilà donc j'ai essayer de faire cette exercice mais je n'y arrive pas c'est un DM de 4 exercice.j'en ai réussi 2. Voilà, Dans le plan muni d'un repère orthonormal (O,i,j), on considère l'hyperbole d'équation y=1/x et la droite D d'équation y=2x-1. Déterminez algébriquement les coordonnées des point...

http://imageshack.us/photo/my-images/835/numriseri.jpg/ Pour la A j'ai trouver A(x)=x(x-2)-2(2x-5) A(x)=x² - (-2x)-4x -(- 10) "C'est "+" direct ici a(x)=x²+6x+10 A(x)=x(x-2)-2(2x-5) A(x)=x² "-" (il sort d'où?) (-2x)-4x - 10) "C'est "+" direct ici a(x)=x² - 6x...

[quote="xJerem47"]Je comprends pas trop =S ... car comment tu a x=1 ou x=-1 ?
sachant que la a) c'est x²-1 x²<1
Donc soit x<*racine* de 1 ou x<-*racine* de 1 !

Capiché ?