Forum de Mathématiques: Maths-Forum

Dlzlogic a écrit:Bonjour,
Je pense qu'il faut déjà "traduire" l'énoncé en expression mathématique.

Justement c'est ce que je n'arrive pas du tout

Bonjour j'aimerais un peu d'aide pour réussir cette algorithme énoncer : f(x) = x² + 5x + 7 / x + 3 g(x) = x+ 2 ecrire un algorithme permettant de calculer l'entier x > 0 pour lequel la distance entre la coubre f et la courbe g est inférieur ou égal à un nombre proche de zéro. coder cette algorithme...

Curlymela a écrit:d'accord merci beaucoup :we:

pour la deuxième question l'énoncer dit si pour tout x > 0 on a 2 + 2/x < ou égale a f(x) < ou égale a 2 + 3/x alors lim f(x) quand x tend vers + l'inf = 2

je pense que la limite de 2+ 2/x = 2 et que la limite de 2 + 3/x = 2 donc lim de f(x) = 2 non ?

Kikoo <3 Bieber a écrit:Si on te dit que blabla est vrai pour toute chose vérifiant truc-bidule, il te suffit de montrer qu'il existe une de ces choses qui ne vérifie pas blabla afin de justifier que cette proposition est fausse.

d'accord merci beaucoup :we:

Curlymela a écrit:mais est-ce que si on donne un contre exemple c'est une vraie justification ?

non on indique pas que f est positif

Curlymela a écrit:d'accord donc -x² est inférieur a 2/x or -x² tend vers - l'infini en l'infini donc f(x) ne tend pas vers 0 pour la condition f(x) inferieur ou egale a 2/x c'est ca ?

mais est-ce que si on donne un contre exemple c'est une vraie justification ?

Oui ! Mais c'est pas ce qu'on te demande. On te demande si tout fonction inférieure ou égale à 2/x tend vers 0 en l'infini. Tu as ta réponse. d'accord donc -x² est inférieur a 2/x or -x² tend vers - l'infini en l'infini donc f(x) ne tend pas vers 0 pour la condition f(x) inferieur ou egale a 2/x c'...

Kikoo <3 Bieber a écrit:Je préfère ça. Donc est-ce que ça tend vers 0 ?

non mais -x² ce n'est pas 2 / x

Curlymela a écrit:Ca veut dire quoi vers plus l'infini en l'infini ?

-x² tend vers - l'infini en l'infini

Kikoo <3 Bieber a écrit:Non non non.
Est-ce que -x² tend vers plus l'infini en l'infini ?

Ca veut dire quoi vers plus l'infini en l'infini ?

Kikoo <3 Bieber a écrit:Comment ça elle n'a pas de limite ?

enfin ca limite serait + l'infini . comment tu répondrais a la question ? j'aurais un exemple pour les autres questions.

Kikoo <3 Bieber a écrit:Considère la fonction .
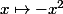
Vois-tu qu'elle est plus petite que la fonction pour tout x de ?
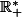
Et pourtant, quel est son comportement en l'infini ?

elle n'a pas de limite

Kikoo <3 Bieber a écrit:Et si ta fonction est continue sur R+ et qu'elle diverge en l'infini ?

je ne comprend pas dsl :help:

[quote="Kikoo 0 , la limite de 2/x quand x tend vers + l'infini sera forcément 0 donc si on prend une fonction égale ou plus petite sa limite sera aussi de 0 non ? La chose que je ne comprend pas c'est que la fonction tend vers 0 en l'infini , cela veut-il dire que quand x tend vers l'infini la...

j'ai pris un exemple vu qu'on sait que x > 0 j'ai pris par exemple x = 2 , je trouve alors f(2) < ou égale a 1 je remarque aussi que plus x est grand plus f(x) se rapproche de 0 donc je pense que la réponse est vraie.

Bonjour j'aimerais quelque explications car je ne comprend vraiment pas cette exercice ou du moins je ne vois vraiment pas comment justifier. Énoncer : Pour chacune de ces affirmations ci-dessous, préciser si elle est vraie ou fausse. Justifier votre réponse. 1) Si pour tout x > 0 , on a f(x) < ou é...

Voila jai un gros problème sur cet exercice est-ce que vous pourrier m'aider s'il vous plait : j'aurais juste besoin d'aide pour l'exercice 4 ( en bas de la page ) : Exercice 3 : Voici un jeu de hasard qui se joue avec une pièce de monnaie et un pion : A partir du sommet 0 (départ) du carré, tu va d...

desoler je ne comprend pas .

donc si j'ai trouver que les solutions pour f(x) etait -3 et 1/2 les solutions pour g(x) sont V-3 et V1/2 . Voila maintenent il dise verifier ces réponses par un calcul jai fait f(0) = 2 X 0² + 5 X 0 -3 = -3 Mais je ne sais pas comment verifier par un calcul pour la solution 1/2 Vraiment desoler de ...

oki merci maintenent je doit faire la meme chose avec g (x) ou pas ?