20 résultats trouvés
Revenir à la recherche avancée
- 16 Sep 2010, 19:37
- Forum: ✯✎ Supérieur
- Sujet: famille de polynômes
- Réponses: 3
- Vues: 1010
famille de polynômes
Bonsoir, je ne comprends pas la résolution de cet exercice. On désignera par E l'espace vectoriel lR[X] des polynômes à une indéterminée à coefficients réels,et par F le sous espace vectoriel de E des polynômes de degré inférieur ou égal à 3. on considère l'application f qui à tout élément P de E as...
- 16 Sep 2010, 19:07
- Forum: ✯✎ Supérieur
- Sujet: famille de polynômes
- Réponses: 3
- Vues: 1010
- 13 Sep 2010, 18:30
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
Ah d'accord on a det1=(3a-2b)d-b(3c-2d)=3ad-3bc det2= bc-ad det3=a(-3c+2d) - c(-3a+2b)=2ad-2bc det1=(3det3)/2 det2=-det3/2 l'énoncé dit de donner la forme générale de l'endomorphisme, donner sa matrice répond à la question?
- 13 Sep 2010, 17:49
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
Je me disais que si f(e1)=\lambda f(e2) donc f(e1) est une combinaison linéaire de f(e2) comme on veut que les vecteurs f(e1)et f(e2) soient indépendants je me suis dit que f(e1)\neq \lambda f(e2) f(e1)=\lambda f(e2) f(e_1) =a\begin{pmatrix}3\\...
- 13 Sep 2010, 17:18
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
Bonjour, Bon j'ai donc la matrice \( \array{3a-2b&3c-2d&\frac{3c}{2}-d&-3a+2b\\b&d&\frac{d}{2}&-b\\a&c&\frac{c}{2}&-a\\-3a+2b&-3c+2d&\frac{-3c}{2}+d&3a-2b\) ai-je donc donc terminé l'exercice? l'énoncé demandant de trouver la forme générale des...
- 13 Sep 2010, 15:36
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 12 Sep 2010, 22:06
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 12 Sep 2010, 21:51
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 12 Sep 2010, 21:40
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
Puis pour les lignes de la matrice j'aurai (e1,e2,e3,e4)?
(e1,e2,e3,e4) est ce la base canonique de l'endomorphisme?
 \in Vect((3,0,1,-3),(-2,1,0,2)))
mais que puis je déduire d'autre?
(e1,e2,e3,e4) est ce la base canonique de l'endomorphisme?
mais que puis je déduire d'autre?
- 12 Sep 2010, 21:08
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
D'accord, et ainsi comment dois-je faire pour trouver la forme générale des endomorphisme vérifiant
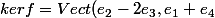)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
(je ne comprends pas trop le terme de forme générale)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
(je ne comprends pas trop le terme de forme générale)
- 12 Sep 2010, 14:52
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
D'accord, et ainsi comment dois-je faire pour trouver la forme générale des endomorphisme vérifiant
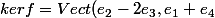)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
(je ne comprends pas trop le terme de forme générale)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
(je ne comprends pas trop le terme de forme générale)
- 12 Sep 2010, 14:01
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 12 Sep 2010, 11:36
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 12 Sep 2010, 10:56
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 12 Sep 2010, 10:06
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 11 Sep 2010, 18:30
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 11 Sep 2010, 10:08
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 10 Sep 2010, 21:33
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
Il faut que l'espace engendré par \{f(e_1),f(e_2),f(e_3),f(e_4)} soit le même que l'espace engendré par \{v_1,v_2\} . =>Vect \{f(e_1),f(e_2),f(e_3),f(e_4)} =Vect \{v_1,v_2\} or\mathrm{Vect}\{f(e_1),f(e_2),f(e_3)...
- 10 Sep 2010, 21:17
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
forme générale d'endomorphismes
Bonsoir, cet exercice m'embête, et je suis complètement à la ramasse Donner la forme générale des endomorphisme de lR ^4 tels que kerf=Vect( e_2-2e_3,e_1+e_4 ) Imf={(x,y,z,t);x+2y-3z=0 et x+t=0} bon j'ai f(e_2) = 2f(e_3) et f(e_4)=-f(e_1) et je bloque :hein: Bonne soi...
- 10 Sep 2010, 20:07
- Forum: ✯✎ Supérieur
- Sujet: forme générale d'endomorphismes
- Réponses: 32
- Vues: 1795
- 20 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
