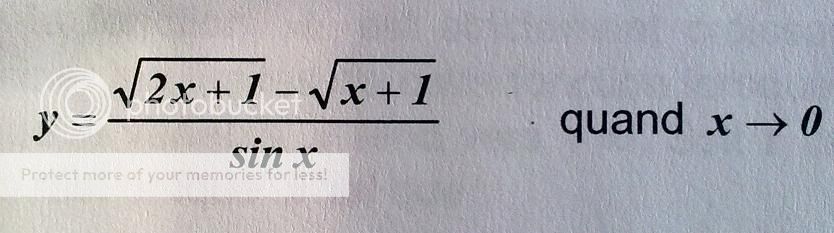Forum de Mathématiques: Maths-Forum

Salut La fonction f est définie par morceaux Pour x [U] 1, f(x) = 2-mx², f est donc continue sur ]1,+oo[ Le seul problème potentiel est x=1 Pour que f soit continue en 1, il faut que la limite à gauche et à droite de f en 1 valent f(1) c'est-à-dire 1-1=0 A gauche c'est donc évident A droite, il fau...

oscar a écrit:f continue


http://yfrog.com/cbimage10g

Désolée Oscar mais ton graphique ne me parle pas :triste:
A quoi correspond a,b et m,M ?

une fonction continue c'est une fonction que l'on pourrait dessiner sans lever le crayon. La fonction que tu as décrite est continue à gauche de 1 et à droite de 1. Reste à montrer qu'au point 1 il n'y a pas de discontinuité et que la valeur donné par les deux expressions est la même. Et donc regar...

Bonjour, Honnêtement je ne comprends rien à la continuité. Je sais ce qu'est une fonction continue (c'est le minimum !) mais quand il s'agit de démontrer qu'une fonction est continue alors là ya plus personne ! ! ! Je sais aussi que : - une somme de fonctions continues est continue - un produit de f...

AH COOL :)

MERCI

Je trouve 1/2 !

C'est bien ça ?

il te suffit de multiplier haut et bas par la quantité conjuguée , c.a.d par \sqrt{2x+1}+\sqrt{x+1} et il n'y aura plus d'indétermination (en se souvenant aussi que la limite de sin x / x est 1) Ah ben écoute j'ai fait ce calcul mais je n'ai pas réussi, je me retrouve toujours avec "quelque ch...

Voilà j'ai fait des tonnes de calculs, je ne sais pas si c'est la fatigue ou moi mais impossible de venir à bout de ce problème :



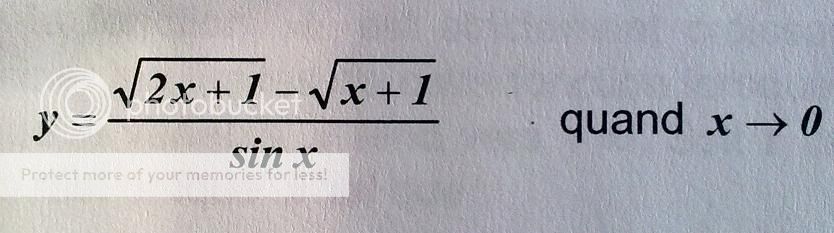
Est-ce que quelqu'un pourrait m'aider, svp

Merci