Forum de Mathématiques: Maths-Forum

Pourrais-je avoir une réponse !

sans vous embeter :s

Mais non la dérivée de (1/4)x c'est 1 plutot non ? car 1/4 se dérive en 0 et x en 1 !

La dérivée de (1/4)x c'est (1/4) non ?

Je vais essayer de la dérivée en entier même si avec les fraction dans le numérateur et le ln(x+1) je crois que ca va pas etre simple :briques:

Merci.

D'accord donc :

F'(x) = x() + ()()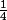

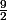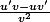avec u(x) = ln(x+1)
v(x) = x
et u'(x)=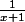
v'(x) = 1

Est ce dans mon u'(x) que j'ai une erreur ?

Merci de m'accorder du temps !

Bonjour ! je m'y suis mise ce matin et donc j'ai commencer à faire comme pour la premiere de l'autre fois ! Soit : Cm(x) = \frac{x}{4} + \frac{9}{2} ( \frac{ln(x+1)}{x} ) Je décompose l'équation en deux soit : - F1(x) = \frac{x}{4} - F2(x) = \frac{9}{2} ( \frac{ln(x+1)}{x} ) Les déri...

Tu as le bouquin déclic seconde ou pas ?
Si c'est celui ci au debut du chapitre tu dois avoir des exos du même genre où tu peux je pense comparer comment ils ont fait !

Tu as cherché les equation de cout total , etc... sur internet !
Je ne les ai pa en tête mais sur internet il doit y avoir ca et apres il te suffit de remplacer je pense !
va voir :we:

Bonjour ! J'ai fini la premiere partie de l'exercice qui en fait était assez simple, je compliquait les choses :marteau: La j'arrive à la partie économique avec une dérivée sacrément difficile je trouve. Et je ne vois même pas quelle forme prendre pour la dérivé. Voici l'énoncé : La fonction coût mo...

Ah d'accord :id:
merci beaucoup !
par contre dans la démonstration on met :

-f est continue sur
-f est strictement croissante sur
Mais pas sur l'intervalle ]0;5] si ?? et elle n'est pas strictement croissante ou strictement décroissante :hum:

Ensuite on me demande de déduire que f s'annule sur ]0;5] pour une valeur unique !

C'est a dire lorque f(x) = 0 ??

oups !

c'est pourtant ce que je faisais mais je ne trouvait pas la même chose lorsque je regardai sur la calculatrice mais j'avais mal tapé ma fonction ! :id:
Désolé !

Merci

ah oui pour (x-2)c'est négatif sur [0;2 ] et positif sur (2;5] ce qui donne pour f'(x) qu'elle est :

-négative sur [0;2]
-positive sur [2;5]
et égale à 0 en 0 et 2 !

Mais où je bloque c'est pour determiner d'apres cela les variations de f(x)

et (x+1) est positif !

On prend le signe de chacun des facteurs

x : +
(x-2) : -
(x+4) : +

donc un facteur est négatif soit un nombre impair de facteurs négatifs.

x(x-2)(x+4) est donc négatif??

Je ne vois vraiment pas comment faire le tableau de variation de f :cry:
Mercii si vous pouvez m'aider !

Je viens de me rendre compte que ma démarche est mauvaise !
ne faut-il pas plutot faire en fonction simplement de f'(x) ? etant donné que f'(x) est positif la fonction f serait positive sur [0;5] .

:hum:

merci d'avance :help:

Bonjour ! en deuxiemement on me demande le tableau des variations de f sur [0;5]. J'ai dit que les variations de f dépendait du signe de la dérivée. J'ai donc dit que (x+1)^2 est toujours positive sur [0;5] ensuite j'ai décomposé le numérateur : x est positive sur [0;5] (x-2) est négative en...

J'ai réussi ! Merci beaucoup !

Car vu que x(x-2)(x+4) = x ( +4x-2x-8)

apres résolution de 'équation de tout à l'heure j'arrive au même résultat :happy2:

C'est encore moi ! lorsque je ré-écrit la fonction avec toutes les dérivées cela me donne : x + \frac{9}{(x+1)^2} - \frac{9}{x+1} = \frac{x(x+1)^2}{(x+1)^2} + \frac{9}{(x+1)^2} - \frac{9(x+1)}{(x+1)^2} et ensuite dois-je continuer le developpement ?

faute d'innatention ! désolé !

Donc f2(x) = 9 / (x+1)²
je vais voir si j'arrive à aller au delà maintenant afin de vérifier par lautre fonction donnée !

Merci beaucoup !