Forum de Mathématiques: Maths-Forum

Bonjour, j'aimerais que vous m'aidiez à trouver la réponse à cette question : Soit T_0^{(1)}= \inf\{n\in\mathbb{N}, X_n=0\} , calculer \mathbb{E}_0(\sum_{k=0}^{T_0^{(1)}-1} \mathbf{1}_{X_k=1234567890}) \mathbb{E}_0(\sum_{n=0}^{T_0^{(1)}-1} \mathbf{1}_{X_n=12345678...

C'est écrit dans l'énoncé... Pas moi !

Montrer que la série converge uniformément vers

Je ne vois pas comment faire pour conclure que le rayon de convergence est supérieur à 1 ?

Mais d'après le cours, le série de fonctions est uniformément convergente si ? Je serais très étonné qu'elle converge uniformément vers et non pas vers 0...

Merci.

C'est une condition nécessaire mais pas suffisante.

Oui, j'ai pas pensé aux conditions où est différent de 0.

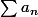converge, ça veut dire que la suite converge vers 0 ?

Bonsoir. Je suis tombé dans un exercice qui demande d'étudier la convergence de la série de fonctions f_k (t) définie par \sum_k \frac{(-1)^k}{2k!} x^{2k} \sin(t)^{2k} Ce qui me laisse penser aux séries entières. En effet, \sum_k \frac{(-1)^k}{2k!} x^{2k} \sin(t&#...

Bonjour. :) J'ai des difficultés, bloqué dans l'exercice suivant : Soit (a_n)_{n \in\mathbb{N}} une suite de nombres réels. A. On suppose que la série de terme général a_n converge, et on note S_n =\sum_{k=1}^{n} a_k . 1)Montrer que les séries entières \sum a_n x^n et \sum S_n x^n ont un ray...