pi a pour équation : -3x+y-2z-1=0
la droite d a comme système d'équations : x-y+z=4 et 2x+3y=1
et un point P (3,2,1)
25 résultats trouvés
Revenir à la recherche avancée
- 18 Oct 2009, 20:05
- Forum: ✎✎ Lycée
- Sujet: géométrie analytique problème
- Réponses: 3
- Vues: 655
géométrie analytique problème
Bonsoir tout le monde. Je dois résoudre un exercice, simplement je ne comprends pas l'énoncé. On me donne les coordonnées de P, l'équation de pi, et les équations cartésiennes de la droite d. On me demande de rechercher le symétrique de P par rapport à d parallèlement à pi. Or, un plan et une droite...
- 18 Oct 2009, 19:42
- Forum: ✎✎ Lycée
- Sujet: géométrie analytique problème
- Réponses: 3
- Vues: 655
Oui, c'est une proposition intéressante. D'ailleurs, en voici une autre : 80^2=b^2+c^2 S=\frac{bc}{2}=\frac{1}{2}(b\sqrt{80^2-b^2}) \frac{dS}{db}=\frac{1}{2}[\sqrt{80^2-b^2}+b\frac{-2b}{2\sqrt{80^2-b^2}}=\frac{1}{2\sqrt{80^2-b^2}}[(80^2-b^2)-b^2]= \frac{80^2-2b^2}{2\sqrt{80^2-b^2}} \...
- 24 Mai 2009, 20:05
- Forum: ✎✎ Lycée
- Sujet: Problème d'optimisation ...
- Réponses: 11
- Vues: 1261
Ericovitchi a écrit:L'aire c'est bc/2, pourquoi multiplies tu par 80 qui est l'hypoténuse ? je ne comprends pas.
Je multiplie, comme le dis la formule, la base (qui vaut 80) par la hauteur (c'est un triangle rectangle, donc l'un des deux côtés de l'angle droit) et on divise le tout par deux.
- 24 Mai 2009, 18:33
- Forum: ✎✎ Lycée
- Sujet: Problème d'optimisation ...
- Réponses: 11
- Vues: 1261
- 24 Mai 2009, 16:20
- Forum: ✎✎ Lycée
- Sujet: Problème d'optimisation ...
- Réponses: 11
- Vues: 1261
- 24 Mai 2009, 14:58
- Forum: ✎✎ Lycée
- Sujet: Problème d'optimisation ...
- Réponses: 11
- Vues: 1261
Problème d'optimisation ...
Bonjour ! J'ai un peu de mal avec le problème suivant : On doit construire une clotûre qui a la forme d'un triangle rectangle, dont l'hypoténuse vaut 80 mètres. Il faut que le terrain délimité par la clotûre ait la plus grande aire possible. Pour l'instant j'ai ceci : sqrt {80}= b^2 + c^2 Aire = \fr...
- 24 Mai 2009, 14:22
- Forum: ✎✎ Lycée
- Sujet: Problème d'optimisation ...
- Réponses: 11
- Vues: 1261
Asymptotes fonctions
Bonjour !
Je bloque un peu sur ces deux exercices ... :
f(x)=
f(x)=
Pour rappel, il faut trouver s'il y a oui ou non des asymptotes, verticales horizontales ou obliques.
Merci d'avance.
Je bloque un peu sur ces deux exercices ... :
f(x)=
f(x)=
Pour rappel, il faut trouver s'il y a oui ou non des asymptotes, verticales horizontales ou obliques.
Merci d'avance.
- 05 Mai 2009, 17:15
- Forum: ✎✎ Lycée
- Sujet: Asymptotes fonctions
- Réponses: 1
- Vues: 562
luly a écrit:Ou alors simplement utiliser la formule de Simpson, ce qui donne :, non ?
Ha mais j'arrive au final à la même réponse :id:
Bon j'vais y aller moi, bonne nuit et merci en tout cas :happy2:
- 26 Jan 2009, 00:02
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
amusante. \displaystyle \frac{sinx}{cosx}-\frac{2 sinx cosx}{cos2x}=sinx on traite sinx=0 puis simplifie par sinx \displaystyle cos2x-2cos^2x=cosxcos2x - 1=cosxcos2x comme les quantités sont entre -1 et 1, nécessairement (cosx=1 et cos2x= -1)ou(cosx=-1 et cos2x=1) Mais aussi non je ne vois pas ce q...
- 25 Jan 2009, 23:46
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
- 25 Jan 2009, 23:20
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
très facile. cos(x)=2cos^2(\frac{x}{2})-1 puis trinôme du second degré de l'inconnue z=cos(\frac{x}{2}) tu peux regarder le calcul d'Oscar (4-\sqrt{2})(4+\sqrt{2})=14 , non ? moi j'ai procédé comme suit : tg x = \frac{v2/4}{1+v2/4} et après simplification, ce...
- 25 Jan 2009, 22:12
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
- 25 Jan 2009, 22:03
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
eh bien, fallait (encore) y penser :marteau:
En sachant que les équations de trigo n'ont plus de secrets pour vous,
en voici une dernière (aller promis, j'en ai plus en stock :happy3:
En sachant que les équations de trigo n'ont plus de secrets pour vous,
en voici une dernière (aller promis, j'en ai plus en stock :happy3:
- 25 Jan 2009, 22:03
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
- 25 Jan 2009, 21:21
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
Re chers amis,
ça vous dirait une petite dernière ?
aller, je vous la donne :zen:
2 cos x + 3 = 4 cos (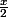 )
)
ça vous dirait une petite dernière ?
aller, je vous la donne :zen:
2 cos x + 3 = 4 cos (
- 25 Jan 2009, 21:11
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
- 25 Jan 2009, 20:54
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
tan(x)=\frac{2\sqrt{2}-1}{7} ps: pour diviser une différence a-b par c , on divise chaque terme par c . a-b:c= \frac{a}{c}-\frac{b}{c} D'accord avec toi pour la divison, mais comment oscar l'applique-t-il ici car de 1) je ne vois pas de différence sauf erreur de ma part et de 2) je ne compr...
- 25 Jan 2009, 19:21
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
Re 2sin x = sin (pi/4-x)= sin pi/4 cos x - sinx cos pi/4 =v2/2) (cos x - sinx) sinx = v2/ 4 ( cos -sinx) sinx + v2/4 sinx = v2/4 cos x sinx ( 1 + v2/4) = v2/4 cos x Diviser les deux memmbres par sinx ( 0) tan x = v2/ ( 4+v2) = v2 ( 4-v2) / 2 On calcule une valeur approchéé puis on détermine la solu...
- 25 Jan 2009, 18:11
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
- 25 Jan 2009, 17:31
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique
- Réponses: 28
- Vues: 1762
- 25 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
