Forum de Mathématiques: Maths-Forum

Je crois que cette fois c'est tout compris. Un grand merci pour votre aide! :happy2:

Salut, ta démonstration est correcte (bien qu'il est inutile de modifier l'expression de l'arctan, vu que sa limite est directement calculable). Visiblement la correction est destinée à des élèves qui n'ont pas étudié les équivalents, qui sont une notion "avancée" : \frac{\sin^2 x^2 Arcta...

benekire2 a écrit:Une question, en quelle classe est tu ?

En fait je n'habite pas en France... mais en Suisse. Je pense que mon niveau correspondrait à terminale scientifique. :hein:
Pourquoi la question?

En faisant comme cela je trouve bien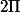

Mais dans les réponses du livre, la marche à suivre est plutôt celle-ci:

Or je ne comprends pas comment ils ont fait?

Bonsoir! J'essaie depuis un bon moment de résoudre cet exercice, sans succès. J'ai la correction (pas très détaillée) mais je ne comprends quand même pas. Est-ce que vous pourriez m'aider s'il vous plaît? \lim_{x \to 0} f(x) f(x) étant: \frac{sin^2(x^2)Arctg(1/x^4)}{(1-co...

!!!!!!!!!!!!!! Il me semble que la dérivée de tan(x) est 1/cos²x !!!!!!!!!!!!!!!! Magie? Alors ce que j'ai trouvé \frac{-1}{sin(x)} est complètement faux... :marteau: Maintenant, oui la dérivée de tan(x) est \frac{1}{cos^2(x)} . Le but de l'exercice est de trouver la primitive de \f...

Merci! Maintenant j'ai compris pourquoi

Mais je ne trouve pas la primitive de . (à moins de chercher dans les tables! )

Parce que j'arrive à : . Et pas à tan(x).

Alors si je dérive tan(x) tan(x) = \frac{sin(x)}{cos(x)} si je dérive ça, j'ai: \frac{cos(x) cos (x) + sin(x) sin(x)}{cos^2(x)} ce qui donne: 1 + \frac{sin^2(x) }{cos^2(x)} qui est égal à 1 + tan^2(x) Soit l'énon...

Bonsoir, je suis en train de répéter pour un test de maths sur les primitives - intégrales. Je bloque à la question: Calculer les intégrales indéfinies: 4) \bigint (1 + tan^2(x)) dx La réponse est tan(x) . Et j'ai essayé plein de formules, je n'arrive pas à ce résultat. J'ai ...