Forum de Mathématiques: Maths-Forum

bonjour,
quelqu'un a t il une idée pour montrer ça SVP?

Bonsoir,
SVP Quelqu'un a t il une idée pour montrer que cette série diverge ?
Un = (-1)^n * ((2n²+1)/n²)

Merci d'avance

fatal_error a écrit:re,

j'ai du mal à comprendre ce que tu veux dire.
Peut etre que ta rédaction éclaircira les choses.

Le critere de D'Alembert dit que si la limite de (Un+1)/Un = k
si k>1 donc diverge
si k<1 donc converge
si k=1 on ne sait pas

on a bien sa avec ((2n²+1)/n²), non?

Bonjour ou Re

Montrer que cette série diverge ?
Un = (-1)^n * ((2n²+1)/n²)

Pour moi on prend ((2n²+1)/n²) qui ressemble au Critère de D'Alembert
et sa limit en infini est 2.
Si sa limite > 1 alors la série diverge.

Ect ce que c'est correct mon raisonnement?

Merci :we:

girdav a écrit:Ce n'est donc pas égal mais équivalent au voisinage de .

Ok précision utile!!! merci

girdav a écrit:Attention au dénominateur! (même si ce qui manque ne joue aucun rôle du point de vue de la convergence )

On peut le négliger!

la série \bigsum \frac{1}{n} diverge. C'est une serie de "référence". Voir la constante d'euler sur wikipedia Edit, comme tu as vu les series de riemann, tu dois aussi savoir que \bigsum \frac{1}{n^{\alpha}} ne converge que pour \alpha \gt 1 Donc (-1)^n / (n² + (-1)^(n+1) ) devient en val...

Ok, dans mon cour, on les appel série harmonique alternée!


est pas convergente, cad 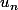n'est pas absolument convergente.


Par contre je ne comprend pas pourquoi en valeur absolue, n'est pas convergente?!

ben donc c'est pas la même chose. Par exemple : pour u_n = \frac{1}{n} \bigsum \frac{(-1)^n}{n} est convergente, mais \bigsum | \frac{(-1)^n}{n}| est pas convergente, cad \bigsum u_n n'est pas absolument convergente. Tu peux commencer par remplacer u_n par |u_n| dans ton exo et voir...

personne sur les suites?! :cry:

Franchement, je me suis posé la même question!!!
Je suppose que c'est juste pour dire convergente mais c'est pas sûr!!!

Dans l'exercice, c'est précisé que (c'est à dire que la série de terme général
lUnl est convergente)

lUnl >>> valeur absolue

Bonjour à tous,


Un= (-1)^n / (n²+(-1)^(n+1)), monter que cette série est absolument convergente

Merci d'avance :hein:

Pour la série, c'est tout simplement

Une condition necessaire est que la limite de u_n en l'infini vaut 0 pour que la serie de terme général u_n converge[/quote]

donc dans notre cas elle est divergente puisque la limit est 1? c'est bien ça? :id:

Personne sur les suites!!!! :cry:

Bonjour tout le monde je voudrais savoir SVP si les affirmations suivante sont vraie ou fausse : 1) La suite de terme général Un = 1 + 1/n est convergente 2) La série de terme général Un = 1 + 1/n est convergente Pour la 1) je dirai que c'est faux car qu'on cherche la limite en , on trouve car 1 + 1...

Et pour 201, on fait comment?!
ya une méthode ou quelque chose?
merci

puisque .[/quote]


Et comment tu trouve ce résultat stp?

z^2009 = (2*e^((-5;))/12))^2009

Et ça fait combien?
:mur:

tu m'etonne avec ton resultat ! ;)/6 - ;)/4 = ;)/12 Non, c'est -;)/6 - ;)/4 = (-5;))/12 tu prend le resultat, tu met l'exposant et tu cherche la valeur principal de l'angles :zen: Non, c'est -;)/6 - ;)/4 = (-5;))/12 donc on cherche juste (;)2/2)^2009? pour la partie exp, on la laisse comme sa?

fourize a écrit:oula ! je n'ai pas fait attention ! (merci yos)

et dire que j'ai dit 103,... :ptdr: :stupid_in

C'est bien ce que je trouve
donc au final, on trouve 2/2*e^((-7;))/12)
(pour 1-i, on trouve -pi/4)


J'aimerai savoir comment faire si on veut cherché :
(;)2/2*e^((-7;))/12))^2009

:id: