51 résultats trouvés
Revenir à la recherche avancée
Re: Separable/ Extension
En fait, j'ai voulu d'abord montrer que si L est un corps (et s'en est un car L/K est une extension finie), alors E := ker(Frob_p −IdA) est un sous-K-espace vectoriel de L de dimension 1. Pour montrer que A = B_1 × · · · B_n (produit de r corps montré à la question précédente), alors E := ker(Frob_p...
- 26 Nov 2020, 21:37
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
Bonjour, Je me permets de faire un petit update parce que je pense avoir trouvé la question suivante. Soit E= ker(Frob_p - Id_a) \subset A Précédemment, on a montré que A est un produit de r extensions finies. E est l'ensemble des racines X^p - X De plus, L/K est une extension finie donc L est un co...
- 26 Nov 2020, 19:01
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
D'accord j'essaye : Soit P=Q_1...Q_r sa décomposition en facteur irréductible dans K[X] . Le théorème des restes chinois affirme que A=\prod_i{K[X]/Q_i} et B_i = K[X]/Q_i est un corps puisque Q_i est irréductible. Donc A est produit de r corps de K et de plus dim_K(A)=n Donc A est produit de...
- 25 Nov 2020, 10:12
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
C'est-à-dire il faut que je montre que  = B_1 * ... * B_r) avec
avec des corps
des corps
On sait que K est un corps car p est premier et P est un polynôme de degré n.
Je ne vois pas comment m'y prendre pour trouver les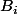 avec
avec 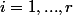
On sait que K est un corps car p est premier et P est un polynôme de degré n.
Je ne vois pas comment m'y prendre pour trouver les
- 24 Nov 2020, 23:17
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
Oui il faut P que soit un polynôme non nul de K[X] et irréductible dans K[X] Donc je pense il faut donc montrer que P est irréductible dans K[X] On pose \alpha = X+(P) On sait que P est séparable c'est à dire \alpha_1 = ...= \alpha_r =1 c'est à dire P est sans facteur carré De plus, soit P=P...
- 24 Nov 2020, 17:40
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
Pardonnez-moi vous avez raison je n'ai pas explicité \alpha_i \alpha=X+ (P) Une base du quotient est (1, \alpha, ..., \alpha^{n-1}) donc dim_K(A)= n (Le degré du polynôme P non nul de degré n) Pour montrer que A est produit de r extensions finies de K : on sait d'après un cor...
- 24 Nov 2020, 10:58
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
Oui c'est vrai ! Pour moi, Z/pZ={0,1,..,p-1} mais je pense donc dire que card(Z/pZ)=p peut-être Oui mais je ne vois pas la dimension de A. Parce qu'une base de K[X] est 1,X,X^2 ,.. K[X] est de dimension infinie. Et P est un polynôme séparable a un degré fini. Si P est séparable par définitio...
- 23 Nov 2020, 21:33
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: Separable/ Extension
Non excusez-moi de K est de caractéristique p je me suis emmêlé. J'ai modifié.
- 23 Nov 2020, 20:53
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Separable/ Extension
Bonjour, J'ai un petit exercice qui me pose problème. Soit K un corps de caractéristique p . Soient K = Z/pZ et P séparable et A = K[X]/(P) 1) Dire que vaut dim_K(A) et montrer que A est produit de r extensions finies de K et que Frob_A est K_linéaire (je rappelle c'est l'application...
- 23 Nov 2020, 19:36
- Forum: ✯✎ Supérieur
- Sujet: Separable/ Extension
- Réponses: 15
- Vues: 557
Re: homéomorphisme
Excusez moi , mais j'ai un doute ! Vous me demandez de montrer que la topologie T_x que je cherche est T_y=T_{eucl} , autrement dit : f (Q^*, T_{eucl}) \rightarrow (Q^*,T_{eucl}) , n'est-ce pas ? Or f=f^{-1} et c'est évident que f est bijective. Donc il y a bien un homéomorphisme pou...
- 29 Oct 2020, 10:58
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
Re: homéomorphisme
Bonsoir, Montrons que T_x= T_y , c'est à dire montrons que T_x et T_y ont les mêmes ouverts. On a montré que f=f^-1 Par conséquent f est bijective (je ne sais pas si j'emploie les bon termes) c'est-à-dire que tout élément appartenant à T_y appartient à T_x autrement dit tout ouvert de T-y appartient...
- 28 Oct 2020, 19:41
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
Re: homéomorphisme
En fait je ne vois as qu'est-ce qu'il va déterminer ma topologie 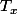 , pouvez-vous m'expliquer s'il vous plaît ?
, pouvez-vous m'expliquer s'il vous plaît ?
- 28 Oct 2020, 17:23
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
Re: homéomorphisme
Exacte !
)=q) donc
donc =f^-1(q))
Mais du coup on me demande de trouver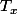 pour laquelle f est un homéomorphisme mais comment le choisir ?
pour laquelle f est un homéomorphisme mais comment le choisir ?
J'avais pensé peut-être à la topologie grossière ...
Mais du coup on me demande de trouver
J'avais pensé peut-être à la topologie grossière ...
- 28 Oct 2020, 15:10
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
Re: homéomorphisme
Bonjour, Je me permets de mettre mes "avancements". Je me suis penchée sur la piste de f^{-1}=f . Je n'arrive pas à le rédiger correctement mais l'idée est que : f : (Q^*, T_x) \rightarrow (Q^*, T_y) tel que q \rightarrow \frac{1}{q} et f^{-1} : (Q^*, T_y) \rightarr...
- 28 Oct 2020, 12:12
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
Re: homéomorphisme
Je le "sens" mais je ne sais pas l'expliquer
- 27 Oct 2020, 12:07
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
homéomorphisme
Bonjour, J'ai une question qui me pose problème. Soient f : (Q^*, T_x) \rightarrow (Q^*, T_y) tel que q\rightarrow \frac{1}{q} et T_y la topologie euclidienne. Vous déterminerez une topologie T_x pour laquelle f est un homéomorphisme. J'ai commencé comme ceci : Une application contin...
- 27 Oct 2020, 11:20
- Forum: ✯✎ Supérieur
- Sujet: homéomorphisme
- Réponses: 10
- Vues: 492
Re: Norme opérateur
Etant donné que j'ai montré qu'on a trouvé une suite non nulle _n=1) tel que
tel que _n)
De plus_n||=1) et
et _n||=1) alors cela implique que
alors cela implique que 
On a montré précédemment que
PAr conséquent
De plus
On a montré précédemment que
PAr conséquent
- 07 Oct 2020, 07:52
- Forum: ✯✎ Supérieur
- Sujet: Norme opérateur
- Réponses: 38
- Vues: 1317
Re: Norme opérateur
Oui c'est vrai je manque de rigueur et je vous remercie de me reprendre et de me corriger pour que je m'améliore sur ce point là ! Par conséquent on a que pour tout entier n, y_n= \frac{1}{n+1}\sum_{k=0}^{n}{1}=x_n Donc on a trouvé une suite non nulle (x_n)_x=1 tel que A(x_n)=x_n c'e...
- 05 Oct 2020, 20:45
- Forum: ✯✎ Supérieur
- Sujet: Norme opérateur
- Réponses: 38
- Vues: 1317
Re: Norme opérateur
Ah et donc si on a ||A|| \leq 1 et ||A||\geq 1 ça veut dire que ||A||=1 Oui je m'excuse j'essaye de faire de mon mieux mais c'est un cours encore très vague pour moi ... Si je prends une suite constante différente de 0 par exemple (x_n)_n=1 alors : A((x_n)_n) = (y_n)_...
- 05 Oct 2020, 19:03
- Forum: ✯✎ Supérieur
- Sujet: Norme opérateur
- Réponses: 38
- Vues: 1317
Re: Norme opérateur
Ah oui ce que vous voulez dire c'est qu'il faut avant de calculer 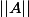 montrer que
montrer que 
Il faut que je trouve une suite tel que :
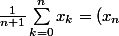_n)
Avec une suite constance cela ne marche pas, je ne vois pas quelle suite_n)
Il faut que je trouve une suite tel que :
Avec une suite constance cela ne marche pas, je ne vois pas quelle suite
- 05 Oct 2020, 15:29
- Forum: ✯✎ Supérieur
- Sujet: Norme opérateur
- Réponses: 38
- Vues: 1317
- 51 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
