Forum de Mathématiques: Maths-Forum

Et bien, on a alors ||B_{p}A-B_{p}|| qui tend vers 0 lorsque p tend vers l'infini (par encadrement), d'où B_{p}A qui tend vers B_{p} Pour faire le lien avec la valeur d'adhérence B , il faut introduire une sous suite extraite, disons B_{p_{\varphi (p)}} qui tend donc vers B. Comme toute suit...

soit

Comment majorer ? Ou du moins ?

Oui pardon pour l'étourderie il y a un facteur 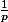devant

Donc

On a après une simplification télescopique
soit sauf erreur de calcul.

Comment exploiter que B est valeur d'adhérence?

On a alors ||B_{p}|| = ||\frac{1}{p} \sum_{k=0}^{p-1}{A^{k}}|| \leq ||\frac{1}{p}\, p\, M|| soit ||B_{p}|| \leq ||M|| donc B_{p} est bien bornée mais du coup, mon majorant de dépend pas de p Si je suis votre raisonnement, il faudrait donc montrer que ||BA-B|| < 0 pour montrer que BA-B=0 c'est bien ça?

Bonjour Je suis face à un exercice de topologie sur les matrices qui me bloque Soient n \geq 1 et A \in M_{n}(C) On suppose que M_{n}(C) est muni d'une norme et que la suite (A^{k})_{k \in N} est bornée. On note pour tout p \geq 1 B_{p} = \frac{1}{p}\sum_{k=0}^{p-1}{A^{k}} Il...