Forum de Mathématiques: Maths-Forum

J'ai pu finir merci

Sa Majesté a écrit:Salut,

Une démonstration par récurrence fonctionne bien.
Tu as déjà fait l'initialisation, reste l'hérédité.

Je suis en première et il ne me semble pas que l'on ait abordé ce terme en cours. Une autre méthode serait-elle possible ?

Bonjour, Voici un exercice : Soit la suite u définie sur \eta par u_{0}=1 et u_{n+1}=\frac{u_{n}}{1+u_{n}(1+2n)} . 1. Calculer les premiers termes de la suite u (on écrira ces termes sous forme de fractions irréductibles). Conjecturer alors une expression explicite de u_{n} . 2. Démontrer la...

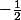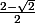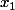Bonsoir, merci je trouve effectivement . J'ai donc pu calculer les racines (qui sont et ) et remplacer et 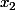par leurs valeurs et je retombe bien sur -1.

Merci de m'avoir aidé

D'autant plus que l'on suppose dans la question 2 que 0

Ok donc (2x_{1}-1)(2x_{2}-1)=-1 \Leftrightarrow 4x_{1}x_{2}-2(x_{1}+x_{2})+1=-1 \Leftrightarrow 4(m+1)-7=-1 \Leftrightarrow 4(m+1)=6 \Leftrightarrow 4m=2 \Leftrightarrow m=\frac{1}{2} Mais après, en calculant le discriminant, on trouve \Delta = -2. On ne peut ...

Alors

Oui en effet car .

A la question 2.a. j'ai trouvé = 2 et = m.

Oui, merci j'ai réussi cette question. Celle qui me pose problème est la question 2. b.

Bonjour, La question 2.b. de l'exercice me pose problème : Soit m , un nombre réel. On considère l'équation : x^{2}-2x+m+1=0 1. Déterminer, suivant les valeurs du réel m , le nombre de solutions de cette équation. 2. On suppose m\leq 0 . a. Déterminer en fonction de m la somme et le produit des raci...