Forum de Mathématiques: Maths-Forum

Il y a par ailleurs une erreur de signe sur un coefficient de la troisième colonne.

Bonjour, Il y a une infinité de matrices orthogonales dont les deux premiers vecteurs colonnes forment une base de F (et les deux derniers, par conséquent , une base de F^\perp ). Ceci justifie le "par exemple", puisque c'est effectivement une possibilité parmi une infinité. La matrice pro...

Bonjour,
Franchement, ce que j'en pense : pipeau !

Tu n'as pas saisi ce que j'ai mis en gras dans mon message. Il y a deux choses complètement différentes : 1°) Le sens dans lequel on parcourt le bord du domaine pour appliquer le théorème des résidus. On le parcourt en laissant à sa gauche l'intérieur du domaine. Donc pour la boucle de rayon r , on ...

Bonsoir, On veut que l'intégrale sur le segment A corresponde à \displaystyle\int_r^R \dfrac{x^p}{1+x^2} . Donc la détermination de z^p sur le domaine à l'intérieur du contour est bien z=\rho e^{i\theta}\mapsto \rho^p e^{ip\theta} où \theta est l'argument entre 0 et 2\pi on arrive bien du côté de B ...

N'as-tu pas vu que j'ai adopté ta "méthode séquentielle" pour l'égalité P(2)=P(3) ? Pour ce qui est de P(1) < P(3) < P(4), ce que j'avais écrit il y a 5 ans est tellement simple et rapide (tu ne trouves pas ?) que je ne vois pas pourquoi je changerais.

Pourquoi faire simple quand on peut faire compliqué ?

Je ne vois pas vraiment, et je n'ai pas plus envie que ça de me creuser la tête. J'ai déjà rappelé plus haut (ça se trouvait dans le fil d'origine, il y a plus de cinq ans) comment on voit sans peine ni calcul que P(1)<P(3)<P(4) . Pour voir P(2)=P(3) , on peut...

Quel est le rapport avec le problème des 8 coeurs ?

Peux-tu répondre sur le sens de ta question trois messages plus haut ?

Je ne comprends pas le sens de ta question.

Soit E l'univers de toutes les distributions possibles. Elles sont équiprobables. Le problème de probabilités est donc en fait un problème de dénombrement. Soit A l'évènement "les 8 coeurs sont chez Yves". Soit B l'évènement "aucun tour n'a les deux cartes de même couleur". Soit...

Une nouvelle fois, je sais bien que le résultat est correct et je peux le démontrer en suivant ce que tu fais. On gagne toujours à expliciter ses arguments, même pour sa propre compréhension. C'est mon expérience personnelle : quand j'écris des maths, je suis parfois tenté d'écrire "il est bie...

Bijection ou pas, ce qui est obligatoire pour justifier une affirmation en mathématiques, c'est une démonstration. "On peut facilement montrer" n'est pas une démonstration. Si c'est facile, on le fait, et de manière compréhensible.

Bonsoir,
Tant qu'à faire @beagle, tu aurais pu mettre le lien sur la discussion à laquelle tu fais allusion :
https://www.maths-forum.com/enigmes/probabilites-liees-independantes-encore-t205531.html
Comme ça chacun pourra se faire son idée, n'est-ce pas ?

Bonsoir,
C'est sans doute plus simple de commencer par s'intéresser à .

Bonjour, Connais-tu la signification de la loi géométrique de paramètre p ? C'est le nombre d'épreuves de Bernoulli indépendantes de paramètre p pour obtenir le premier succès (revois ton cours pour vérifier !) L'évènement X\geq k , ça veut dire que les k-1 premières épreuves sont ratées. Probabilit...

Bonsoir,
Ce que tu appelles degré n'est pas clair. Quel est le degré du polynôme ? Le degré total ? le degré par rapport à ? par rapport à ? Ou est-ce un couple ? Mezalor quel est le monôme de plus grand degré dans ce polynôme ?

L'arbre est simple : au premier tirage, 3 possibilités A, B et C. Si A ça s'arrête, gagnant pour A. Partant de chacun des noeuds B et C trois branches A, B, C. On s'arrête pour les noeuds BB et CB, gagnants pour B. Partant de chacun des noeuds BA, BC., CA, CC de nouveau trois branches A, B, C. On s'...

Bonsoir,
Je te suggère de nommer les nombres de boules 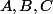et de faire un arbre où tu feras figurer toutes les histoires possibles, avec les probabilités calculées en fonction de à chaque embranchement.