Forum de Mathématiques: Maths-Forum

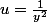
J’ai posé et j’ai résolu l’équation différentielle, il me reste le début de la question 2), c’est-à-dire « Montrer que si , non identiquement nulle, est solution de alors ne s’annule pas.»

Si quelqu'un pouvait m'aider.
Merci d’avance.

Ta note est 0/20 pour cet epsilon de la question 1) car tu ne démontres rien du tout. La question 1) nous demande de préciser cet intervalle de {{\mathbb{R}}^{*}} , toi tu donnes \mathbb{R} comme intervalle. C’est juste que \left\{ \begin{aligned} & x\to 0 \\ & \mathbb{R}\to \mathbb{R} \\ \e...

Est une solution maximale.

Sur où sur , car il y a unicité de la solution.

On dit que (y,I) est une solution maximale d’une l'équation différentielle si elle n'admet pas de prolongement. Autrement dit, pour toute autre solution.
Si et pour tout alors

En math parfois on a besoin même de comprendre la solution de l’exercice. Et c’est le cas ici, je cherche une solution pour la comprendre, dans l’autre forum je suis sûr à 100% que c’est faux. Et si tu crois que c’est juste, cela veut dire que toi-même tu n’as pas compris et tu as besoin de qu’un qu...

Mon avis personnel c’est que tu n’aides pas les gens, mais au pire tu compliques leurs problèmes. La preuve : dans le cas de mon exercice et comme tu as vu que j’ai déjà été dans d’autres forums et ça n’allait pas, si tu as envie d’aider c’est d’expliquer en détail la première question, chose que ta...

Bonsoir, Monsieur il me provoque avec des messages et puis il supprime. Je suis venu ici pour l’aide, il n’est pas capable de m’aider et il n’a pas le niveau pour ça, de plus il a vu que j’ai déjà été dans un autre forum là où je n’ai rien compris, alors il me suit ici pour me perturber encore. Donc...

Tu as baissé le niveau dans ton deuxième message effacé en plus. OK, on peut comprendre que tu as effacé ton premier message, que tu crois qu’il s’agit d’une aide (c’est effacé dans ma tête avant que tu l’effaces).

Je suis désolé, mais c’est toi qui as baissé le niveau dans ton deuxième message. Un conseil : n’aide plus personne, car : 1- Tu ne sais rien du tout et vas apprendre les maths avant de venir ici. 2- On va supposer que tu sais un peu en math, franchement va faire autre chose que venir aider dans des...

On ne peut pas répondre à la question si l’on ne résout pas l’équation. Tout ce qu’on peut dire c’est ce que j’ai écrit à 00 :21 À part ça, donne-moi cet intervalle, toi qui prétends comprendre la solution maximale du théorème de Cauchy. Si tu penses que c’est faux ce que j’ai écrit à 00:21, ça ne s...

La réponse à la question 1) je l’ai écrit à 00:21 ( et je suis sûr de ce que j’écris ). Et ceci montre que je connais ce que ça veut dire une solution maximale. Je pense que tu es un des deux débiles qui se trouve dans l’autre forum, sinon tu vas être un nouveau de ce forum. Non, je ne vais pas à bi...

1- Sur l’autre forum, je n’ai pas confiance de ce qui raconte ces deux personnes 2- Je n’ai pas compris ce qui me raconte 3- Les informations je les ai trouvées tout seul. 4- Je sais très bien repérer si l’aide que je reçois est logique et correcte ou pas. 5- Jusqu’au présent je n’ai pas reçu d’aide...

Bonsoir et merci pour la réponse. D’après le théorème de Cauchy-Lipschitz, le problème de Cauchy admet une seule solution maximale. Donc : Si y_0=0 , cette solution maximale est : x\to 0 Définie sur \mathbb{R}_{-}^{*} si {{x}_{0}}<0 Définie sur \mathbb{R}_{+}^{*} si {{x}_{0}}>0 Je pense que c’est to...

Bonjour, je suis bloqué dans le début de cet exercice si vous pouvez m’aider. Soit le problème de Cauchy ( E ) : xy'+y=xy^3 avec la condition initiale y(x_0)=y_0. . 1)vérifier qu’il existe une solution maximale de ( E ) sur un intervalle de \mathbb{R}^* à préciser. 2)Mont...