Forum de Mathématiques: Maths-Forum

Ce n'est pas les racines, c'est juste les valeurs de x à rejeter, qui ne sont pas dans le domaine. Car tan de n'importe quel x ne peut pas être égale à la tan de 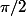, elle n'existe pas, les droites ne se coupent pas car elles sont parallèles.

Ah d'accord, je m'en doutais, c'est pour ça que j'ai modifié un peu le message mais bon, au moins, maintenant c'est clair

Qui te dis que c'est positif, la fonction \tan varie de -\infty à +\infty Parce que -\infty^2=+\infty Je te rappelle tan^2x , autrement dit, (tan x)^2 , forme qui rend l’opération du calcul plus facile à comprendre, l’opération du carré vient à la fin. Donc même si la \lim_{x\rightarrow \pm...

Hello, Pour les valeurs d'annulation du dénominateur, j'aurais fait comme toi. 6tanx/(1-tan^2) - tan x = 0 Ssi: 6tan x - tan x (1 - tan^2) = 0 5 tan x + tan^3 (x) = 0 Ssi Tan x (5 + tan ^2 x) = 0 Dans la parenthèse c'est toujours positif strictement donc (ssi, x étant réel) Tan x = 0 C'est pas bon....

Merci beaucoup, par contre, est-ce qu'il y a toutes les conditions d'existence ou est-ce que j'en aurai omises ?

Domaine \ ?

Alors, j'ai un exercice où l'on me demande de trouver le domaine et les racines des fonctions suivantes. Le problème étant que je n'aie jamais été bon en trigonométrie, bref ... f (x) = \frac{tan 2x}{3tan 2x - tan x} C.E. : tan 2x \neq tan \pi/2 \Leftrightarrow 2x \neq\pi/2 +k\pi\Leftrightarrow x \n...