Forum de Mathématiques: Maths-Forum

Oui alors voilà ce que j'ai trouvé pour le premier : 2^{n}\equiv -1 \left[3 \right] je sais pas si ça peut servir sinon pour le deuxième j'ai plus : La somme est égale à \frac{n(n+1)(2n+1)-6}{6} = \frac{(n-1)(2n^{2}+5n+6)}{6} et on a pgcd((n-1);(2n^{2...

Oui alors voilà ce que j'ai trouvé pour le premier : 2^{n}\equiv -1 \left[3 \right] je sais pas si ça peut servir sinon pour le deuxième j'ai plus : La somme est égale à \frac{n(n+1)(2n+1)-6}{6} = \frac{(n-1)(2n^{2}+5n+6)}{6} et on a pgcd((n-1);(2n^{2}...

Bonjour, est ce que quelqu'un pourrait m'aider ?
Montrez que si divise alors est divisible par .
Et aussi
Trouvez les entiers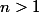 pour lesquels la somme est une puissance d'un nombre premier.
Merci