Forum de Mathématiques: Maths-Forum

Pourquoi jusqu'à \sqrt{n^2+2n+1} ? Tu sais que c'est "k allant de 1 à ..." ? Oui mais comme les terme s'arrêtaient toujours à \sqrt{n^2+2n+1} j'avais pensé que peut être que c'est possible :gene: Je peux te dire que c'est: S_n = \sum_{k=1}^{2n+1} {\frac{1}{\sqrt{n^2+k}}} Quand n = 1 on va...

Le sujet est fermé comme je dois le rendre à la première heure de cours x) merci beaucoup pour tout bonne journée! ^^

Mdrr :D d'accord d'accord je crois comprendre le truc mais ca va faire un quelque chose de bizarre donc je sens le faux quand même . Comme tu m'as donné la somme de S1 je réutilise pour Sn ce qui fait Sn = \frac{1}{\sqrt{n^2+k}} et comme tu as mentionné le dernier terme de Sn dans l'énoncé alors peu...

Sn = \sum_{k=2}^{n}{n^2} ou \sum_{k=2}^{n}{k^2} Je n'ai jamais vraiment compris les calcules avec les sommes sauf si il s'agit de somme arithmétique et géométrique :oops: Arrête d'aller à la pêche et réfléchis ! Tu as des racines d'un côté (et l'expression de Sn t'es donné dans l'énoncé quand même ...

Tu cliques sur éditeur d'équations et tu veras comment ca fonctionne par contre si tu veux mettre un carré ou un nombre en puissance tu fais comme à la calculatrice "^2" mais sinon c'est pas grave merci

Bon aller j'abandonne. Merciii vraiment pour tout ca m'a beaucoup aidé ^^ bonne soirée et continuation

\sqrt{n^2+1} = n\sqrt{1+\frac{1}{n^2}} =n En calculant la formule que tu m'as écrit j'ai retrouvé ce résultat. Euh pourquoi égal? En tout cas tu peux utiliser la même logique que dans l'autre. Il te reste qu'à factoriser par n en haut aussi puis simplifier et trouver le limite du soutien ! \frac{2n...

Sn = \sum_{k=1}^{n}{\frac{1}{\sqrt{k^2+1}}}+\frac{1}{\sqrt{k^2+2}}+ \frac{1}{\sqrt{k^2+3}}+...+\frac{1}{\sqrt{k^2+2k+1}} ? Toujours à la pêche à ce que je vois. Le principe utiliser le symbole somme c'est ce ne plus avoir les "...". Tu n'as jamais fait ce genre de trucs? Si je te dis Sn= ...

\sqrt{n^2+1} = n\sqrt{1+\frac{1}{n^2}} =n En calculant la formule que tu m'as écrit j'ai retrouvé ce résultat. Euh pourquoi égal? En tout cas tu peux utiliser la même logique que dans l'autre. Il te reste qu'à factoriser par n en haut aussi puis simplifier et trouver le limite du soutien ! \sqrt{2n...

Bonne nuit ^^

En calculant la formule que tu m'as écrit j'ai retrouvé ce résultat.

Pour la deuxième limite, ce serait bien de savoir comment tu as fait la première déjà ! Le plus classique sera d'utiliser: \sqrt{n^2+1} = n \sqrt{1 + \frac{1}{n^2}} La première j'ai tous factoriser par n en haut et en bas puis ensuite les n disparaissent et j'ai appliqué mes connaissances sur les l...

C'est presque ça (l'expression d'il y a 2 messages) pour Sn. Je t'invite à checker S1, S2, S3. D'ailleurs j'ai mis que ça commençait à k=0 mais c'est pas forcément vrai :D Concernant la limite oui c'est bien 2 et si tu le fais bien, l'autre terme aussi tend vers 2 ! D'accord :D je mettrais 1 car ça...

Leona17 a écrit:je crois que j'ai compris peut être :



Si vraiment ça passe pas on peut laisser tomber si vous voulez

C'est celui la ou j'y suis presque ?

sinon pour la 2eme limite ça me complique avec les racines mais j'ai fais : \frac{2n+1}{\sqrt{n^2+1}} = \frac{(\sqrt{n^2+1)} (2n+1)}{(\sqrt{n^2+1)}(\sqrt{n^2+1)}} = \frac{(\sqrt{n^2+1)} (2n+1)}{n^2+1} après je sais plus quoi faire ni même si c'est bon...

?

je crois que j'ai compris peut être :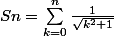



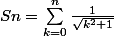
Si vraiment ça passe pas on peut laisser tomber si vous voulez

Sn = \frac{1}{n+1} + \frac{1}{(n+1)^2} + \frac{1}{\sqrt{n+1}}+ \frac{1}{\sqrt{(n+1)^2}} ? Ensuite, j'ai trouver une méthode pour calculer les forme indéterminés sur internet http://labomath.free.fr/faidherbe/premS/limite/limites.pdf dans le 4-; 3) sur la 2eme page donc pour les limi...

XENSECP a écrit:

Leona17 a écrit:En calculant S1 tu retrouves les résultats sous quel forme ? C'est ça qui t'aidera ^^"

Alors tu en es où?

Moi ? ^^"