Forum de Mathématiques: Maths-Forum

chan79 a écrit:Salut
Au fait, la fonction g, c'est quoi ?

La fonction g est :

mathelot a écrit:la limite est infinie en

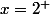
Oui mais je dois trouver la dérivée en 2 et une fois sur deux je trouve sois :
g'(2)=0 ou g'(2)= impossible ?
Merci

mathelot a écrit:utiliser le LaTeX ou les parenthèses

est-ce

?

Désolé je n'avais pas compris comment utiliser le Tex. C'est cette formule ci dessous :

Bonjour !
J'ai une petite question pour pouvoir continuer sereinement mon exercice.
g'(x) = 2(racine de 2x-4) + 4x/2(racine de 2x-4)
Je dois trouver la dérivée en 2.
Je n'arrive pas a savoir si g'(2) est impossible ou si g'(2)=0.
Merci.

J'ai donc essayé et j'ai trouver que le signe de f'(x) était donc décroissante sur [-pi/2 ; pi/2] mais ce résultat me semble étrange..
Pour ce qui est de la parité, puis-je avoir une explication ? Pourquoi est-elle impair ?
Merci pour vos réponses.

Bonjour, j'aurais besoin d'aide pour un exercice de terminale S. Soit f définie sur [ -pi/2 ; pi/2] par f(x)= xcos(x) - 2sin(x) 1. Etudier la parité de f. 2. Montrer que f est dérivable sur [-pi/2;pi/2] et calculer f'(x) 3. Dresse le tableau de variation de f'(x) Ce que j'ai fait : 1. Pour tout réel...