8 résultats trouvés
Revenir à la recherche avancée
zygomatique a écrit:y = (a + b)x - ab
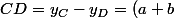c - ab - c^2 = \frac {(a - b)^2}{4} - (c - \frac {a + b}{2})^2)
ce qui permet de répondre au problème ...
Merci beaucoup pour toute votre aide,
Lywet
- par lywet
- 05 Jan 2015, 18:59
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
j ai finalement trouvé le polynome:
-xc²+(a+b)xc-ab
Les coordonnées du sommet de la parabole sont (alpha, beta)
j'ai trouvé alpha= (a+b)/2
mais pour beta je trouve : -((a+b)²-4ab)/-4)
Or cela ne correspond pas si l on prend des exemples...
Merci de votre aide
- par lywet
- 04 Jan 2015, 18:34
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
equation de la droite:
y=(xa+xb)x-xaxb
Abscisse de C
yc=(xa+xb)x-xaxb
Ordonnée de c:
y=(xa+xb)xc-xaxb
?
- par lywet
- 03 Jan 2015, 13:55
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
mais lis-tu ce qu'on écrit ? .... :mur: x_d = x_c !!!!!!!!!!!! ensuite il serait peut-être bien de calculer y_c en fonction de x_c !!!!!!!!!!!! oui j ai compris que xd avait la meme abscisse que xc, mais ils n'ont pas la meme ordonnée, xd² n est pas égal à xc² Biancoangelo a écrit: Il faut écrire C...
- par lywet
- 03 Jan 2015, 13:38
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
d accord, je vois mon erreur.
mais du coup (xc-xc)² cela fait 0, il ne reste donc que (xd²-yc)² ?
CD= racine de (xd²-yc)²
CD=xd²-yc ?
- par lywet
- 02 Jan 2015, 21:24
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
oui pas de problème :)
l'équation de AB est donc:
y=(xb+xa)x - xaxb
les coordonnées de c sont donc
y=(xb+xa)xc - xaxb
D (xc,xd²)
distance CD:
CD=(xc-xc)²+(xc²-xc²)² ?
- par lywet
- 02 Jan 2015, 20:12
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
Tu pourrais établir l'équation de la droite (AB) avec A(x_A,x_A^2) et B(x_B,x_B^2) puis prendre un point C d'abscisse x_C (x_A\leq x_C\leq x_B) appartenant à cette droite et établir les coordonnées de D puis la distance CD Grace à votre conseil, j'ai pu trouver: A (xa;xa²) B...
- par lywet
- 02 Jan 2015, 19:44
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954
bonjour, je suis élève de première S. Notre professeur de mathématiques nous a donné un problème ouvert pendant les vacances, mais je n'arrive pas à le résoudre. Voila le problème: On considère la parabole P d'équation y=x² A et B sont deux points distincts de cette parabole. C est un point du segme...
- par lywet
- 02 Jan 2015, 17:05
-
- Forum: ✎✎ Lycée
- Sujet: Problème ouvert
- Réponses: 18
- Vues: 954