Eh bien voilà!
de rien et bonne soirée à toi aussi
3131 résultats trouvés
Revenir à la recherche avancée
- 15 Mai 2025, 17:09
- Forum: ✎ Collège et Primaire
- Sujet: Trigonométrie et Pythagore niveau 4eme !
- Réponses: 6
- Vues: 1388
Re: Trigonométrie et Pythagore niveau 4eme !
Ok pour la figure Il n'y a pas besoin de repère. Le point D est le symétrique du point A par rapport à O. Ou si tu préfères , D est le point d'intersection du prolongement de AO avec le cercle C. La résolution demande uniquement de connaître le fait que tout angle inscrit dans un demi-cercle est dro...
- 15 Mai 2025, 15:05
- Forum: ✎ Collège et Primaire
- Sujet: Trigonométrie et Pythagore niveau 4eme !
- Réponses: 6
- Vues: 1388
Re: Trigonométrie et Pythagore niveau 4eme !
Si j'ai la même image que toi?, tu peux construire 2 triangles rectangles, sachant que tout angle inscrit dans un demi-cercle est droit:
1°) AMD : avec A, M donnés dans l'énoncé et D(-1;0)
2°) ANO avec A,N donnés dans l'énoncé et O(0;0)
et ensuite appliquer dans chaque triangle le lemme
1°) AMD : avec A, M donnés dans l'énoncé et D(-1;0)
2°) ANO avec A,N donnés dans l'énoncé et O(0;0)
et ensuite appliquer dans chaque triangle le lemme
- 15 Mai 2025, 12:29
- Forum: ✎ Collège et Primaire
- Sujet: Trigonométrie et Pythagore niveau 4eme !
- Réponses: 6
- Vues: 1388
Re: Trigonométrie et Pythagore niveau 4eme !
Bonjour,
On a pas l'image!
On a pas l'image!
- 15 Mai 2025, 09:19
- Forum: ✎ Collège et Primaire
- Sujet: Trigonométrie et Pythagore niveau 4eme !
- Réponses: 6
- Vues: 1388
- 03 Mai 2025, 22:24
- Forum: ⚔ Défis et énigmes
- Sujet: Question de cercle tangent à 2 paraboles
- Réponses: 16
- Vues: 834
Re: Question de cercle tangent à 2 paraboles
Bonjour GaBuZoMeu,
j'ai procédé comme catamat; connaissant a,b et c, j'ai calculé r
Pourrais-tu nous dire comment tu as obtenu directement une équation en r?
Merci d'avance
j'ai procédé comme catamat; connaissant a,b et c, j'ai calculé r
Pourrais-tu nous dire comment tu as obtenu directement une équation en r?
Merci d'avance
- 03 Mai 2025, 20:03
- Forum: ⚔ Défis et énigmes
- Sujet: Question de cercle tangent à 2 paraboles
- Réponses: 16
- Vues: 834
Re: Question de cercle tangent à 2 paraboles
OK ; maintenant nous trouvons la même chose; quant à résoudre le système d'équations "à la main" ce n'est pas évident; je crois que c'est impossible sans passer par un logiciel du genre de Wolfram
- 03 Mai 2025, 10:38
- Forum: ⚔ Défis et énigmes
- Sujet: Question de cercle tangent à 2 paraboles
- Réponses: 16
- Vues: 834
Re: Question de cercle tangent à 2 paraboles
Bonjour,
@catmat : es-tu sûr de l'expression de l'équation de la normale ,par exemple, au point A ?
@catmat : es-tu sûr de l'expression de l'équation de la normale ,par exemple, au point A ?
- 02 Mai 2025, 17:47
- Forum: ⚔ Défis et énigmes
- Sujet: Question de cercle tangent à 2 paraboles
- Réponses: 16
- Vues: 834
Re: Calcul d’une intégrale
Bonjour,
on peut décomposer comme suit:
(x^6+1)}=-\dfrac{x-1}{6(x^2+\sqrt{3}\,x+1)}-\dfrac{x-1}{6(x^2-\sqrt{3}\,x+1)}-\dfrac{x-1}{6(x^2+1)}+\dfrac{1}{2(x+1)})
ensuite, on intègre terme à terme
on peut décomposer comme suit:
ensuite, on intègre terme à terme
- 01 Mai 2025, 19:17
- Forum: ✯✎ Supérieur
- Sujet: Calcul d’une intégrale
- Réponses: 1
- Vues: 1294
Re: Question de cercle tangent à 2 paraboles
Bonjour,
le fait que le centre du cercle soit situé sur l'axe des abscisses, est-ce une donnée ou c'est toi qui l'a supposé?
le fait que le centre du cercle soit situé sur l'axe des abscisses, est-ce une donnée ou c'est toi qui l'a supposé?
- 30 Avr 2025, 16:15
- Forum: ⚔ Défis et énigmes
- Sujet: Question de cercle tangent à 2 paraboles
- Réponses: 16
- Vues: 834
Re: Comment exprimer une équation en utilisant des hypothèse
Bonjour,
Je n'ai peut-être pas compris, mais essaies-tu de tirer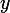 en partant de
en partant de 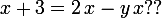
Je n'ai peut-être pas compris, mais essaies-tu de tirer
- 28 Avr 2025, 16:29
- Forum: ⚜ Salon Mathématique
- Sujet: Comment exprimer une équation en utilisant des hypothèses do
- Réponses: 3
- Vues: 435
Re: Question de Géométrie
tu as raison pour MB, erreur de recopie, de ma part
pourquoi remplacer x par 1?
l'expression 6+4x est plus probable que racine de 9+x²+ 2x + 3 ??
le périmètre vaut
pourquoi remplacer x par 1?
l'expression 6+4x est plus probable que racine de 9+x²+ 2x + 3 ??
le périmètre vaut
- 09 Mar 2025, 23:51
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
AMND : tu t'es trompé en recopiant
BCNM c'est faux, il manque MB

BCNM c'est faux, il manque MB
- 09 Mar 2025, 23:29
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
Périmètre AMND : tu peux encore regrouper des termes
Revois un peu le périmètre de BCNM ( j'ai repris les points dans l'ordre demandé, même si ça ne change pas le résultat )
Revois un peu le périmètre de BCNM ( j'ai repris les points dans l'ordre demandé, même si ça ne change pas le résultat )
- 09 Mar 2025, 23:09
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
OK
donne un peu les différents périmètres
donne un peu les différents périmètres
- 09 Mar 2025, 22:52
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
avant le calcul du périmètre occupe toi de la partie A, si tu as des réponses tu devrais les donner
- 09 Mar 2025, 22:19
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
je ne comprends pas ta réponseEltarrion3 a écrit:Bonjour,
Et bien oui mais le problème étant que si j'utilise " racine de 9+x² ", et bien impossible d'avoir une un expression valide avec des x².
pourrais-tu détailler?
Pisigma a écrit:
as-tu déjà répondu à la question 2?
- 09 Mar 2025, 22:00
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
je ne comprends pas ta réponse
Pisigma a écrit:
as-tu déjà répondu à la question 2?
- 09 Mar 2025, 21:58
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
de quelle question parles-tu?
as-tu déjà répondu à la question 2?
as-tu déjà répondu à la question 2?
- 09 Mar 2025, 21:42
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Re: Question de Géométrie
Bonjour,
oui c'est correct
Eltarrion3 a écrit:alors le résultat est racine de 9+x² ?
oui c'est correct
- 09 Mar 2025, 21:12
- Forum: ✎✎ Lycée
- Sujet: Question de Géométrie
- Réponses: 30
- Vues: 3430
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
