37 résultats trouvés
Revenir à la recherche avancée
- 02 Mai 2014, 14:27
- Forum: ✯✎ Supérieur
- Sujet: Matrice, division euclidienne...
- Réponses: 4
- Vues: 1013
- 02 Mai 2014, 09:32
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Pour la formule générale j'aurais pu l'écrire selon a et d par exemple ou b et c ? Le plus important c'est de l'écrire que suivant 2 paramètres ? Oui c'est enfin fini, en tout cas merci beaucoup pour votre aide, je pense que seule je n'y serais pas arrivée. C'est très gentil de m'avoir suivie tout a...
- 01 Mai 2014, 21:52
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Ok merci je vais essayer de compléter donc B_{3n-1} = J ^n Pour B_{3n} : B_{3n} = B_{3n-1} + (A^{3n}) Comme on sait que I_3 = A ^{3n} alors on a B_{3n-1} + I_3 = J ^n + I_3 Pour B_{3n+1} : B_{3n+1}=B_{3n}+A^{3n+1} = B_{3n} + (A^{3n})*A = J^n + I_3 + A Est- ce juste ? Je n'ai pas beso...
- 01 Mai 2014, 21:49
- Forum: ✯✎ Supérieur
- Sujet: Matrice, division euclidienne...
- Réponses: 4
- Vues: 1013
AH oui mince merci, donc j'ai a=1, b=-2, c=1 et d=-1 donc j'ai comme matrice vérifiant * : A= \left(\begin{array}{l}1 -2\\1 -1\end{array}\right) Pour la formule générale j'ai essayé de suivre vos conseil j'ai exprimé a en fonction de d et c en fonction de a et b et j'ai : A=(-d b) (-1-d²)/b ...
- 01 Mai 2014, 21:15
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Matrice, division euclidienne...
http://img11.hostingpics.net/pics/987583Screenshot20140501130231.jpg Bonjour, J'aimerais un peu d'aide svp pour la dernière question de cet exercice J'ai démontré la 1ère, pour la 2 j'ai explique les différents restes (0,1,2) selon que k=3p, k=3p+1, k=3p+2 (dans N) Et à la question 3 dans Z j'ai fa...
- 01 Mai 2014, 12:08
- Forum: ✯✎ Supérieur
- Sujet: Matrice, division euclidienne...
- Réponses: 4
- Vues: 1013
Ok c'est pas grave merci.
Mais il y a quelque chose qui doit m'échapper parce que quand je prend a= 1, b=-1, c=2 et d=-1 ça ne vérifie pas A²=-In <=>
a²+bc= -1
b(d+a)=0 donc a+d=0
a(c+d)= -1
d²+bc=0
Je me suis peut etre trompée dans les équations alors.
Mais il y a quelque chose qui doit m'échapper parce que quand je prend a= 1, b=-1, c=2 et d=-1 ça ne vérifie pas A²=-In <=>
a²+bc= -1
b(d+a)=0 donc a+d=0
a(c+d)= -1
d²+bc=0
Je me suis peut etre trompée dans les équations alors.
- 01 Mai 2014, 11:41
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 01 Mai 2014, 09:29
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 30 Avr 2014, 18:27
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Comment on peut savoir que I_2 ne vérifie pas * ? Son déterminant est bien (-1)n pourtant ? Donc j'ai A= \left(\begin{array}{l}a b\\c d\end{array}\right) A²=-I= \left(\begin{array}{l}a2 +bc / b(a+d)\\a(c+d) / d2+cb\end{array}\right)* (?=puissance) J'ai posé : a²+bc...
- 30 Avr 2014, 17:32
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Bon j'ai det(A)=1 puisque det(A)²=1
Après j'ai cherché une matrice A quelconque vérifiant * mais en fait j'ai trouvé que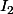 peut vérifier * puisque son déterminant est 1. Mais après je pense que c'est faux parce qu'ensuite je ne peux pas généraliser.
peut vérifier * puisque son déterminant est 1. Mais après je pense que c'est faux parce qu'ensuite je ne peux pas généraliser.
Après j'ai cherché une matrice A quelconque vérifiant * mais en fait j'ai trouvé que
- 30 Avr 2014, 11:43
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 29 Avr 2014, 22:14
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Ah ok je n'y aurais pas pensé, je me complique la vie à chaque fois j'ai l'impression Je comptai mettre au carré ma formule :ptdr: Merci beaucoup Manny et Thomas. Il faut absolument que je trouve la dernière question parce que sinon j'ai l'impression que c'est vous qui me faites tout le boulot j'...
- 29 Avr 2014, 22:02
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
J'ai det(I)=1 mais par contre det(A²) je vois pas quoi mettre à part det(A²)=detA*detA et detA= 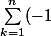k+1*ak1*det(M_k,1)) (le ? est une puissance je sais pas pourquoi on me met ça quand je veux mettre ce sigle :
(le ? est une puissance je sais pas pourquoi on me met ça quand je veux mettre ce sigle :
si on développe selon la 1ère colonne de la matrice
si on développe selon la 1ère colonne de la matrice
- 29 Avr 2014, 17:43
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 28 Avr 2014, 19:44
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 28 Avr 2014, 17:38
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 28 Avr 2014, 14:55
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 28 Avr 2014, 08:44
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Donc à la question b) je suis censée dire que le fait de trouver la famille libre (u,v,f(u),f(v)) dans R3 est impossible ?
- 27 Avr 2014, 21:49
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
Ah oui d'accord je n'avais pas vu qu'à la b) quand on dit que la famille (u,v,f(u),f(v)) est libre, on est pas dans R3, ce ne sont que u et v qui appartiennent à R3. Parce que sinon ça aurait fait une famille de 4 vecteurs libre dans R3 et je comprenais plus rien là :doh: XD Ok merci j'ai compris ma...
- 27 Avr 2014, 20:24
- Forum: ✯✎ Supérieur
- Sujet: Matrice et applications linéaires
- Réponses: 70
- Vues: 3959
- 37 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
