Forum de Mathématiques: Maths-Forum

kelthuzad a écrit:Ok alors c'est
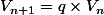
Ce que t'as écrit était faux.

Ah, autant pour moi, et le calcul est bien mené ?

kelthuzad a écrit:Salut,


Non... C'est comme écrire x = 1/2 * x c'est une équation qui a que 0 comme solution.
Calcule Un en fonction de n dans un premier temps.

j'ai eu le même type d'exercice en cours, et j'ai recopié, de la même manière ...

Désolé, mais j'ai encore un souci, 3) Montrer que la suite Vn est géométrique J'ai fait : La suite semble être de raison 1/2 Nous devons démontrer que Vn = q * Vn, Vn = 1/2 * Vn = (1/2) Un + 2n-1 - 4(n+1) +10 = (1/2) Un +2n -1 - 4n - 4 + 10 = (1/2) Un +2n-1 -4n -4 +10 = (1/2) Un -2n +5 Et là je suis...

kelthuzad a écrit:C'est effectivement ça. Tu n'as plus besoin de nous maintenant.

Merci pour votre aide :++:

kelthuzad a écrit:Tu remplaces tous les n par 1, tu devras donc remplacer U1 par sa valeur.

Pour v1 je trouve 7
et v2 3.5

ça parait logique non ? :hein:

Thomas Joseph a écrit:C'est correct

Et pour calculer V1 ? :hein:

Thomas Joseph a écrit:bien sûr

Donc :

Vn = Un - 4n + 10
V0 = U0 - 4*0 + 10
V0 = 4 + 10
V0 = 14 ? :hein:

Pourriez vous juste me lancer sur la question suivante ? :we:

2) On pose pour tout entier n, Vn = Un - 4n + 10
Calculer V0, V1 et V2

Je fais comment ? Comme avant ? :hum:

chan79 a écrit:c'est bien ça

Merci, ça me paraissait juste un peu étrange :ptdr:

chan79 a écrit:ça fait bien 1

Merci, mais pour la 2, c'est là que je bloque un peu, mon résultat parait bizarre

u2 = (1/2) * 1 + 2*1 -1
u2 = (1/2) + 1
u2 = (1/2) + (2/2)
u2 = 3/2 ? :hein:

Thomas Joseph a écrit:Il faut remplacer par 0.

Donc je fais :

u1 = (1/2) * 4 + 2*0 -1
u1 = (4/2) -1
u1 = (4/2) - (2/2)
u1 = 2/2 = 1 ? :hein:

Bonjour à tous :++: J'ai du mal avec l'exercice 2 de mon DM, le voici : On définie la suite (Un) par : u0 = 4 et pour tout entier n supérieur ou égal à 0, Un+1= 1/2 Un+2n-1 1) Calculer u1 et u2 J'ai un pb pour ce calcul : u1 = u0 + 1 = (1/2) * 4 + 2n - 1 Ici je remplace le n par 1 ou 0 ? :hum: Merci

paquito a écrit:Non, c'est immédiat.

Merci bien :++:

Carpate a écrit:b) donc de signe ...
Conclusion ?

Ah d'accord, mais il n'y a donc pas de calcul à faire ? :we:

Bonjour à tous :lol3: Je commence mon Devoir Maison de mathématiques sur les suites aujourd'hui et je suis un peu perdu, voici l'énoncé de l'exercice 1 : Déterminer les variations des suites suivantes : a) Un = n²+3n+1 b) Un+1 = Un -2n Pour la A, je crois avoir compris, il faut faire Un+1 - Un, mais...