Trigonométrie

[M4tidde]

Bonjour

Soit z = exp(i*theta) avec - pi < theta < pi
Est-il possible de trouver un argument de 1+z ?

Cordialement

[aviateur]

Bonjour Oui cela doit être possible. je pose a l'argument de 1+z
Méthode 1.
Par le calcul: écrire 1+z sous forme cartésienne x+iy et on a tan(a)=y/x , donc mettre y/x sous forme d'une tangente.

Méthode 2 (plus simple) Faire un dessin en plaçant les points 0, 1 et 1+z. Ils forment un triangle isocèle
en 1. Repérer les angles theta et a sur la figure et on voit facilement le résultat.

[samoufar]

Bonjour,

Une autre façon de procéder est de faire ce que l'on appelle une factorisation par l'angle moitié. Tu as

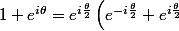Ensuite tu disposes de l'identité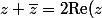 , qui permet de simplifier ce qu'il y a entre parenthèses. Enfin, il reste à en vérifier le signe, pour ajouter ou non un déphasage de .

[aviateur]

Rebonjour
Oui analytiquement la méthode de @samoufar est vraiment ce qu'il y a de plus simple.

[M4tidde]

Merci à tous !

[M4tidde]

Rebonjour,

Finalement, cela me donne arg(2*Re(z)*exp(i*theta/2)) = arg(2)+arg(cos(theta/2))+arg(exp(i*theta/2))
= 0 + theta/2 (2pi) + theta/2 (2pi) = theta + 2*k*pi ?

Cordialement,

[mathelot]

l ' erreur est dans la lecture graphique (appliquer la règle d'addition des vecteurs , la règle du parallèlogramme)

[mathelot]

arg(cos(theta/2))
= 0 ou pi car le cosinus est un réel

[M4tidde]

Donc ça me donne arg(1+z) = pi + k*pi + thêta/2 + 2*k*pi = thêta/2 + (3k+1)*pi ?

[aviateur]

Bonjour
Je reprends la factorisation de Samoufar qui donne

donc

Ainsi et (on peut ajouter 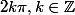si on veut pour obtenir tous les arguments mais ce n'est pas demandé)

Mais une démonstration géométrique n'est pas inutile car elle donne l'argument pratiquement directement.

[M4tidde]

Merci bien !

[zygomatique]

salut

peu de réflexion, de savoir et d'effort ...

1/ que vient faire ce sujet dans le forum orientation ?

2/ tout nombre complexe non nul possède un argument ... donc tout nombre complexe augmenté de 1 possède un argument ...

3/ qu'il est évidemment aisé à calculer avec un peut d'effort et de travail ...