Bonjour,
Je suis en totale galère sur un exercice. Pouvez-vous m'aider ?
Voici l'énoncé:
1-On considère la suite (vn) définie pour tout entier naturel n, par: vn=(Un)/(1-un) sachant que Un=(4x)/(1+3x)
a)Montrer que la suite (vn) est géométrique de raison 4. En déduire pour tout entier naturel n, l'expression de vn en fonction de n
b)Démontrer que, pour tout entier naturel n, on a :un=(vn)/(vn+1)
c) Montret alors que, pour tout entier naturel n, on a : (Un)= 1/(1+0,25puissance n)
Retrouver par le calcul la limite de la suite (Un)
Suites
Règles du forum
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
4 messages
- Page 1 sur 1
Re: Suites
Bonjour,
qu'est-ce que les x viennent faire dans ton énoncé ?
Quelle est la vraie définition de Un
qu'est-ce que les x viennent faire dans ton énoncé ?
Quelle est la vraie définition de Un
Re: Suites
Bonsoir,
Il faut lire
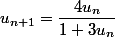
On peut reconstituer cette définition en utilisant les résultats à démontrer
il ne manque plus que la valeur de (1er terme de la suite (u)).
(1er terme de la suite (u)).
je penche pour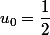
Il faut lire
On peut reconstituer cette définition en utilisant les résultats à démontrer

il ne manque plus que la valeur de
je penche pour
Modifié en dernier par mathelot le 04 Déc 2021, 18:30, modifié 2 fois.
Re: Suites
Question 1.a
 est fonction de
est fonction de  , donc:
, donc:
 est fonction de
est fonction de  (même formule au rang n+1)
(même formule au rang n+1)
 est fonction de
est fonction de  (formule de récurrence pour la suite u)
(formule de récurrence pour la suite u)
 est fonction de
est fonction de 
d'où
 est fonction de
est fonction de 
il faut traduire tout cela par des calculs et trouver au final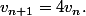
remarque: comment inverser une relation homographique ? :
a,b,c,d,x et y sont des nombres réels, on suppose a*d-b*c non nul:
si on a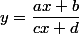 , il vient:
, il vient:
=ax+b)
=b-dy)
donc
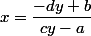
ces calculs permettent d'inverser la relation qui lie x et y.
Au début du calcul , y est fonction de x et à la fin, x est fonction de y.
remarque 2: est un nombre réel. C'est l'image de l'entier n par la fonction u:
est un nombre réel. C'est l'image de l'entier n par la fonction u:
) noté
noté 
d'où
il faut traduire tout cela par des calculs et trouver au final
remarque: comment inverser une relation homographique ? :
a,b,c,d,x et y sont des nombres réels, on suppose a*d-b*c non nul:
si on a
donc
ces calculs permettent d'inverser la relation qui lie x et y.
Au début du calcul , y est fonction de x et à la fin, x est fonction de y.
remarque 2:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
