Bonjour je n'arrive pas du tout à faire cet exercice par manque de notions et je ne trouve pas sur internet des cas presque semblable au mien.
1. Soit f(x) = arcsin x + arccos x.
(a) Déterminer le domaine de définition Df .
(b) Calculer f'(x) pour tout x ∈] − 1, 1[.
(c) En déduire que, pour tout x ∈ [−1, 1], on a : f(x) = π/2
Merci d'avance.
Etude de Fonction
Règles du forum
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
Cette section est un espace convivial permettant aux nouveaux de se présenter.
Merci de ne pas poser des questions mathématiques dans cette section !
6 messages
- Page 1 sur 1
Re: Etude de Fonction
Bonjour,
Question 1 : domaine de définition de f:
si y=arcsin(x), alors le sinus de y vaut x.
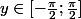
A quel intervalle appartient x ?
si y=arccos(x), alors le cosinus de y vaut x.
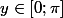
A quel intervalle appartient x ?
question 2 : dérivée de f:
Dérivée de arcsin:
y=arcsin(x)
=x)
en dérivant par rapport à x:
=1)
})
}})
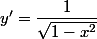
=\dfrac{1}{\sqrt{1-x^2}})
Dérivée de arccos:
y=arccos(x)
=x)
en dérivant par rapport à x:
)=1)
})
}})
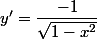
=\dfrac{-1}{\sqrt{1-x^2}})
Que vaut la dérivée de f ?
Question 1 : domaine de définition de f:
si y=arcsin(x), alors le sinus de y vaut x.
A quel intervalle appartient x ?
si y=arccos(x), alors le cosinus de y vaut x.
A quel intervalle appartient x ?
question 2 : dérivée de f:
Dérivée de arcsin:
y=arcsin(x)
en dérivant par rapport à x:
Dérivée de arccos:
y=arccos(x)
en dérivant par rapport à x:
Que vaut la dérivée de f ?
Re: Etude de Fonction
Bonjour,
pour le 1) je pense que la fonction est comprise entre -1 < x <1
et pour le 2) la dérivée devrait être 0
Merci d'avance pour vos réponses
pour le 1) je pense que la fonction est comprise entre -1 < x <1
et pour le 2) la dérivée devrait être 0
Merci d'avance pour vos réponses
Re: Etude de Fonction
Bonsoir,
le domaine de définition de f est [-1;1] et son domaine de dérivabilité est ]-1;1[ à priori
effectivement, la dérivée de f est nulle sur ]-1;1[
le domaine de définition de f est [-1;1] et son domaine de dérivabilité est ]-1;1[ à priori
effectivement, la dérivée de f est nulle sur ]-1;1[
Re: Etude de Fonction
soit g une fonction dérivable sur un intervalle ouvert I non vide
on suppose que g'=0 sur I. Que peut-on dire de g?
réponse: g est constante sur l'intervalle ]-1;1[ puis par continuité sur l'intervalle [-1;1]
on a donc arcsin(x)+arccos(x)=constante
en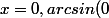=0)
en=\frac{\pi}{2})
donc=\frac{\pi}{2}) pour
pour 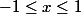
on suppose que g'=0 sur I. Que peut-on dire de g?
réponse: g est constante sur l'intervalle ]-1;1[ puis par continuité sur l'intervalle [-1;1]
on a donc arcsin(x)+arccos(x)=constante
en
en
donc
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
