Petit problème avec une équation caractéristique

par **Aktar** » 23 Juil 2013, 18:27

Bonjour,

Je ne suis pas très fort en math et j'ai un problème qui semble tout bête mais que je n'arrive pas à résoudre. J'ai l'inverse de mon équation caractéristique.

avec L l'opérateur lag. Je souhaite travaillé avec les racines caractéristique et je définie donc

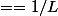
car sinon j'ai l'inverse de mes racines...

Dans mon bouquin on me dis que l'équation caractéristique peut s'écrire sous la forme suivante:

J'ai beau développer je n'arrive pas à retrouver le polynôme de degré 2.

Est-ce que quelqu'un peut m'aider svp.

Merci beaucoup

par **Black Jack** » 23 Juil 2013, 18:48

Aktar a écrit:Bonjour,

Je ne suis pas très fort en math et j'ai un problème qui semble tout bête mais que je n'arrive pas à résoudre. J'ai l'inverse de mon équation caractéristique.

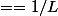
avec L l'opérateur lag. Je souhaite travaillé avec les racines caractéristique et je définie donc car sinon j'ai l'inverse de mes racines...

Dans mon bouquin on me dis que l'équation caractéristique peut s'écrire sous la forme suivante:

J'ai beau développer je n'arrive pas à retrouver le polynôme de degré 2.

Est-ce que quelqu'un peut m'aider svp.

Merci beaucoup

Cela me semble quasi immédiat.

L = 1/Lambda et donc (1-a11.L).(1-a22.L)-a12.a21.L² = 0 peut s'écrire :

(1 - a11/Lambda).(1 - a22/Lambda) - a12.a21/Lambda² = 0

(Lambda - a11)/Lambda * (Lambda - a22)/Lambda - a12.a21/Lambda² = 0
(Lambda - a11)*(Lambda - a22)/Lambda² - a12.a21/Lambda² = 0 (et comme Lambda n'est pas nul --->)
(Lambda - a11)*(Lambda - a22) - a12.a21 = 0
Lambda² - Lambda*a22 - Lambda*a11 + a11.a22 - a12.a21 = 0
Lambda² - Lambda*(a11+a22) + a11.a22 - a12.a21 = 0

:zen:

par **Aktar** » 23 Juil 2013, 19:09

Black Jack a écrit:Cela me semble quasi immédiat.

L = 1/Lambda et donc (1-a11.L).(1-a22.L)-a12.a21.L² = 0 peut s'écrire :

(1 - a11/Lambda).(1 - a22/Lambda) - a12.a21/Lambda² = 0

(Lambda - a11)/Lambda * (Lambda - a22)/Lambda - a12.a21/Lambda² = 0
(Lambda - a11)*(Lambda - a22)/Lambda² - a12.a21/Lambda² = 0 (et comme Lambda n'est pas nul --->)
(Lambda - a11)*(Lambda - a22) - a12.a21 = 0
Lambda² - Lambda*a22 - Lambda*a11 + a11.a22 - a12.a21 = 0
Lambda² - Lambda*(a11+a22) + a11.a22 - a12.a21 = 0

:zen:

ok merci beaucoup... je remplaçais L par

et non pas par

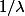
:mur:. Par contre je ne comprends pas comment tu fais disparaitre le

... c'est simplement parce qu'on pose = 0 ? et du coup ça ne change rien à l'égalité?

par **Luc** » 23 Juil 2013, 20:15

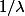
Aktar a écrit:ok merci beaucoup... je remplaçais L par et non pas par :mur:. Par contre je ne comprends pas comment tu fais disparaitre le ... c'est simplement parce qu'on pose = 0 ? et du coup ça ne change rien à l'égalité?

En fait il a juste tout multiplié par

à gauche et à droite de l'égalité. Ça ne change rien à l'égalité car

est non nul.

par **Aktar** » 24 Juil 2013, 10:50

Ok merci beaucoup,

Dans mon exemple on appelle

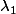
la première racine carac. et

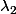
la deuxième racine carac.
J'en profite donc pour vous demander comment on peux passer de l'équation caractéristique à

sachant que

...

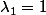
J'ai beau retourner le truc dans tous les sens je vois pas :cry:

Merci

par **spike0789** » 24 Juil 2013, 13:05

Bonjour,

Au vu des messages précédents, j'ai l'impression que tu ne fais aucun effort. C'est pourtant exactement la même chose que précédemment...

Tu es d'accord à dire que le polynôme caractéristique (que je note

) est de la forme :

?

(C'est un polynôme de degré 2 avec coefficient dominant égal à 1. J'imagine la matrice dans

et donc 2 racines réelles car 1 en est une)

Comme

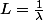
, on a

et on multiplie par L² pour trouver

Finalement,

Reste plus qu'à remplacer

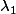
par 1

par **Aktar** » 24 Juil 2013, 13:29

spike0789 a écrit:Bonjour,

Au vu des messages précédents, j'ai l'impression que tu ne fais aucun effort. C'est pourtant exactement la même chose que précédemment...

Tu es d'accord à dire que le polynôme caractéristique (que je note ) est de la forme : ?

(C'est un polynôme de degré 2 avec coefficient dominant égal à 1. J'imagine la matrice dans et donc 2 racines réelles car 1 en est une)

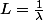
Comme , on a

et on multiplie par L² pour trouver

Finalement,

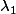
Reste plus qu'à remplacer par 1

Merci,

je n'ai jamais fais d'équation différentielle et je ne savais pas qu'on pouvait écrire le polynôme de cette façon. J'aurais pu chercher encore des heures sans trouver. Merci en tout cas.

par **spike0789** » 24 Juil 2013, 13:40

Je t'en prie, mais ce n'est pas une équation différentielle... :triste:

C'est la forme factorisée d'un polynôme (vue en seconde). Un polynôme P de degré deux admet deux racines

et

(complexes ou réelles) et sa forme factorisée est :

avec k coefficient dominant.

Et on voit bien que

et

...

par **Aktar** » 24 Juil 2013, 13:50

spike0789 a écrit:Je t'en prie, mais ce n'est pas une équation différentielle... :triste:

C'est la forme factorisée d'un polynôme (vue en seconde). Un polynôme P de degré deux admet deux racines et (complexes ou réelles) et sa forme factorisée est :

avec k coefficient dominant.

Et on voit bien que et ...

ok, j'aurais du faire option maths :cry:

je m'en mords les doigts aujourd'hui. Connais-tu un bon cours ou un bon livre sur l'algèbre polynomial?

par **spike0789** » 24 Juil 2013, 13:52

Tout se rattrape ne t'inquiète pas :lol3:

Alors niveau bouquin, non pas vraiment désolé mais cela dépend de ton niveau ET du niveau recherché. Je connais des livres de niveau Maths Spé très bien.

par **Aktar** » 24 Juil 2013, 14:06

j'ai un niveau très bas et je souhaite avoir un niveau terminal S pour commencer.

par **spike0789** » 24 Juil 2013, 14:19

OK désolé de ne pouvoir t'aider. :triste:
Je ne connais pas de livres de TS...

par **spike0789** » 24 Juil 2013, 14:21

Mais tu pourras toujours poser tes questions sur le forum (je te conseille néanmoins la section lycée si les questions concernent des points vus au lycée) :)

Petit problème avec une équation caractéristique

petit problème avec une équation caractéristique

Qui est en ligne