[integrales]Révision
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
maxmaxmax
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Juil 2006, 19:34
-
 par maxmaxmax » 21 Aoû 2006, 20:07
par maxmaxmax » 21 Aoû 2006, 20:07
salut,
Ce serait bien si vous pouviez me donner quelques exercices d'intégrales comme ça je peux les refaire ici et vous pourriez me corriger histoire de voir si je suis prêt pour mon examen de repassage.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2006, 20:13
par Nightmare » 21 Aoû 2006, 20:13
Bonsoir
Quels types d'exercice ?
Calcul d'intégrales ? Etude d'une suite ou d'une fonction définie par une intégrale ? Problème qui revient au calcul d'intégrale ?
-
maxmaxmax
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Juil 2006, 19:34
-
 par maxmaxmax » 21 Aoû 2006, 21:35
par maxmaxmax » 21 Aoû 2006, 21:35
intégrales simples
du style
cos 5x = sin 5x
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2006, 21:39
par Nightmare » 21 Aoû 2006, 21:39
"cos 5x = sin 5x"
C'est une intégrale ça ? J'appelle ça une équation ...
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 21 Aoû 2006, 21:58
par ayanis » 21 Aoû 2006, 21:58
surtout que c'est une composée donc la primitive de cos(5x) c'est 1/5 sin(5x), mais bon...
ttyl
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2006, 22:04
par Nightmare » 21 Aoû 2006, 22:04
ayanis a écrit: la primitive de cos(5x) c'est 1/5 sin(5x)
Beurk :censure:
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 21 Aoû 2006, 22:17
par ayanis » 21 Aoû 2006, 22:17
Nightmare a écrit:Beurk :censure:
Pourquoi beurk? je me suis trompée? c'est possible, mais dans ce cas il faut vraiment que j'aille me coucher parce que je la vois pas...
see u
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2006, 22:47
par Nightmare » 21 Aoû 2006, 22:47
J'aurais plutot dit :
"une primitive de x->cos(5x) est x->1/5 sin(5x)"
C'est là tout :lol3:
-
maxmaxmax
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Juil 2006, 19:34
-
 par maxmaxmax » 26 Aoû 2006, 18:53
par maxmaxmax » 26 Aoû 2006, 18:53
mais ou vous allez chercher le 1/5 vous ???
cos 5 x intégré ça vaut 5 sin x
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 26 Aoû 2006, 19:09
par nekros » 26 Aoû 2006, 19:09
maxmaxmax a écrit:mais ou vous allez chercher le 1/5 vous ???
cos 5 x intégré ça vaut 5 sin x
Ah bon, pour toi la dérivée de
)
est
)
!!!
On a plutôt
)'=5cos(x))
Dérive
)
pour voir ... :lol4:
A+
-
maxmaxmax
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Juil 2006, 19:34
-
 par maxmaxmax » 27 Aoû 2006, 19:51
par maxmaxmax » 27 Aoû 2006, 19:51
oups j'ai oublié le 5
sin 5 x ça donne - cos 5 x jpense car on inverse le signe
-
maxmaxmax
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Juil 2006, 19:34
-
 par maxmaxmax » 27 Aoû 2006, 19:52
par maxmaxmax » 27 Aoû 2006, 19:52
mais je parle pas de dérivation je parle d'intégration
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 27 Aoû 2006, 20:02
par nekros » 27 Aoû 2006, 20:02
Connais-tu la définition d'une primitive ?
Une primitive d'une fonction

est une fonction

telle que pour tout

, la dérivée de
)
est égale à
)
Tu me dis qu'une primitive de
)
est
)
Note
=sin(5x))
et
=-cos(5x))
Alors normalement
=sin(5x))
Or,
=5sin(5x) \neq sin(5x))
C'est pour ça qu'on multiplie par

Je te conseille de revoir la dérivation d'une fonction de la forme
))
ou
))
. :lol4:
A+
-
maxmaxmax
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Juil 2006, 19:34
-
 par maxmaxmax » 30 Aoû 2006, 17:48
par maxmaxmax » 30 Aoû 2006, 17:48
ah ok g capté
en fait quand il y a un nombre à coté de x c'est pas le meme que quand il est tout seul car ça devient une fonction le 1/5 annule le 5
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 30 Aoû 2006, 17:54
par nekros » 30 Aoû 2006, 17:54
Bah une primitive de
)
est
)
A+
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 30 Aoû 2006, 18:05
par B_J » 30 Aoû 2006, 18:05
salut

Voici un theoreme tres important :
Soit

une fonction dont on connait une primitive

et soit
)
une fonction derivable alors toute primitive de la fonction de

:
] \times u'(x))
est
]+C)
avec

une constante reelle.
Exemple :
calculer les primitives de
=cos(x) \times [sin(x)]^4)
?
Reponse :
posons
 =sin(x))
alors
=cos(x))
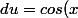dx)
et les primitives de

sont
= \int {f(x)dx}=\int {u^4 du}= \frac{1}{5} \times [u(x)]^5 +C =\frac{1}{5} [sin(x)]^5 +C)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 30 Aoû 2006, 18:06
par fonfon » 30 Aoû 2006, 18:06
Salut, pour le calcul de primitive
si f(x)=cos(ax+b) (a#0) (a,b cstes) alors une primitive est F(x)=(1/a)sin(ax+b)
si f(x)=sin(ax+b) (mm cond pour a,b) alors une primitive est F(x)=(-1/a)cos(ax+b)
.... il y en a bcq à connaître
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 30 Aoû 2006, 18:09
par B_J » 30 Aoû 2006, 18:09
Cas particulier important : si
=ax+b)
alors
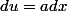
et
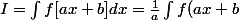 \times a \times dx}=\frac{1}{a}\int {f(u)du}<br />=\frac{1}{a}F(ax+b) +C)
avec

une primitive quelconque de

-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 30 Aoû 2006, 18:16
par B_J » 30 Aoû 2006, 18:16
Voici quelques exemples :
1)
dx} = \frac{1}{5}x^5 - \frac{3}{4} x^4 +2x^3-2x^2 -x +C)
2)
^7 dx} = \frac{1}{2} \int{u^7 du} = \frac{1}{2} \times \frac{1}{8} \times u^8 +C =<br /> \frac{1}{16} (2x+5)^8 +C)
3)
 dx} = \int {(x^3-3+ \frac{4}{x^2})dx } = \frac{1}{4} x^4 -3x - \frac{4}{x}+C)
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 30 Aoû 2006, 18:22
par B_J » 30 Aoû 2006, 18:22
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
 est une fonction
est une fonction  telle que pour tout
telle que pour tout  , la dérivée de
, la dérivée de ) est égale à
est égale à )
) est
est )
=sin(5x)) et
et =-cos(5x))
=sin(5x))
=5sin(5x) \neq sin(5x))

)) ou
ou )) . :lol4:
. :lol4: