Cela fait plusieurs heures que je cherche à exprimer
Merci d'avance.
Somme finie
3 messages
- Page 1 sur 1
Somme finie
par Farwell » 20 Mai 2013, 18:05
Bonjour,
Cela fait plusieurs heures que je cherche à exprimer))
avec 
Un coup de pouce serait le bien venu.
Merci d'avance.
Cela fait plusieurs heures que je cherche à exprimer
Merci d'avance.
par Kikoo <3 Bieber » 20 Mai 2013, 19:07
Salut,
Alors déjà on va commencer par enlever la sommation :
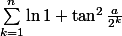\)=\ln\(\prod_{k=1}^n 1+\tan^2\(\frac{a}{2^k} \)\)=\ln\(\prod_{k=1}^n \frac{1}{\cos^2\(\frac{a}{2^k} \)}\)=-\ln\(\prod_{k=1}^n \cos^2\(\frac{a}{2^k} \)\))
Maintenant il faut remarquer que cos(a/2)=sin(a)/2sin(a/2) ce qui te fait :
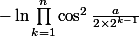\)=-\ln\(\prod_{k=1}^n \frac{\sin^2\(\frac{a}{2^{k-1}}\)}{4\sin^2\(\frac{a}{2^{k}}\)\)=-\ln\(\frac{\sin^2(a)}{ 4^n\sin^2\(\frac{a}{2^n}\)}\)=-2\ln\(\frac{\sin(a)}{ 2^n\sin\(\frac{a}{2^n}\)}\))
PS : J'ai pas vu ton message, xensecp ! Je viens de poster ce que j'avais écrit avant d'aller manger.
Farwell a écrit:Bonjour,
Cela fait plusieurs heures que je cherche à exprimer
Merci d'avance.
Alors déjà on va commencer par enlever la sommation :
Maintenant il faut remarquer que cos(a/2)=sin(a)/2sin(a/2) ce qui te fait :
PS : J'ai pas vu ton message, xensecp ! Je viens de poster ce que j'avais écrit avant d'aller manger.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :