F(x)=12

par **juudu62** » 11 Avr 2013, 09:15

Archibald a écrit:Bonjour,

alors, plusieurs choses à dire :

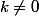
1) Quand tu as plusieurs expressions d'une fonction et qu'on te demande sa dérivée, toujours prendre l'expression la plus simple. En l'occurrence, l'expression polynomiale que tu vas pouvoir dériver en une étape. Tu sais que : avec et . A toi de dériver cette fonction maintenant.

2) pour étudier le tableau de signe d'une fonction affine
Le sens de variation de ta fonction dépend du coefficient directeur a : si a > 0, ta fonction est strictement croissante, elle va du négatif au positif. Si a < 0, c'est l'inverse.
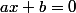
L'endroit où elle change de signe, c'est-à-dire, est donné par

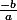
j'ai jamais apprit ça moi !!
Je vais te donner un exemple pour être plus clair : imaginons qu'après avoir dérivé ta fonction f, tu obtiens . Tu as
Le coefficient directeur de ta droite a est négatif donc tu en déduis que ta fonction dérivée est décroissante : elle va du positif au négatif. Et tu sais qu'elle change de signe en (f'(2)=0 donc)
Tu peux alors construire le tableau de signe de ta dérivée f' : elle est de signe + sur ]-infini,2[ et de signe - sur ]2,+infini[
Après avoir fait ce tableau, tu peux en déduire le tableau de variation de f , qui est croissante là où sa dérivée est de signe + (donc sur ]-infini,2[) et décroissante là où sa dérivée est de signe - (donc sur ]2,+infini[)

donc
(- 2x ² + 2x + 12)'=
-2*(x²)'+2*(x)'+(12)'= (d'après le tableau)
-2*2x + 2 +0 = -4x+2

par **Sylviel** » 11 Avr 2013, 09:17

petite remarque pour Archibald : pourquoi mettre des contraintes sur k et n dans ta formule ?

Sinon je répète ma remarque : tu décomposes trop ton calcul et donc tu t'y perds et fait plein d'erreurs. Je vais écrire des choses que les prof n'aiment pas pour te faire comprendre le calcul (sur un exemple comparable) :

(3x²-5x+25)' =(3x²)' - (5x) ' + (25) ' (car (u+v)'=u'+v' )
= 3(x²)' - 5(x) '+0 (car (ku)'=k u', et la dérivée d'une constante est 0)
= 3*2x - 5 (car la dérivée de x² est 2x et la dérivée de x est 1)
= 6x -5

essaie de le faire sur ton exemple.

Et sinon je te ferais remarquer que tu n'as toujours pas fait le 1) que je t'ai demandé et ai passé directement au 2 :marteau:

EDIT : bien tu as réussi à faire le calcul que je voulais te voir faire dans ce message :-)

par **Archibald** » 11 Avr 2013, 09:23

juudu62 a écrit:Etape n°1 : - 2*x ² + 2*x + 12 est de la forme u + v avec u = - 2*x ² et v = 2*x + 12 or (u + v)' = u' + v'

Etape n°2 : - 2*x ² est de la forme u * v avec u = - 2 et v = x ²
or (u * v)' = u' * v + u * v'

Etape n°3 : 2*x + 12 est de la forme u + v avec u = 2*x et v = 12 or (u + v)' = u' + v'

Etape n°4 : 2*x est de la forme ku
or (ku)' = k u' avec k = 2 et u = x

f(x)= -2+2 non ?

Tu n'as pas besoin de toutes ces étapes de justification. Tes profs ne sont pas idiots, ils connaissent la dérivée d'une somme ou d'un produit. Tu dois pouvoir passer directement de f à f'. Bien sûr, si ca t'aide, tu écris tes formules sur ton brouillon pour ne pas faire d'erreurs.

Donc, tu sais que(x^2)'=2x d'où -2(x^2)'= (-2)x(2x) = ...

par **juudu62** » 11 Avr 2013, 09:26

donc a = -4 et b=2
Le coefficient directeur de la droite a est négatif donc tu j'en déduis que la fonction dérivée est décroissante : elle va du positif au négatif. Et elle doit change de signe en -b/a = -2/-4 (f'(0.5)=12.5) non ?

je peux alors construire le tableau de signe de la dérivée f' : elle est de signe + sur ]-infini,0.5[ et de signe - sur ]0.5,+infini[
Après avoir fait ce tableau, je peux en déduire le tableau de variation de f , qui est croissante là où sa dérivée est de signe + (donc sur ]-infini,0.5[) et décroissante là où sa dérivée est de signe - (donc sur ]0.5,+infini[0.5

c'est correcte ?

par **Archibald** » 11 Avr 2013, 09:30

Sylviel a écrit:petite remarque pour Archibald : pourquoi mettre des contraintes sur k et n dans ta formule ?

Sur n parce que c'est comme ca qu'ils ont l'habitude de leur apprendre au lycée. Pour qu'ils ne passent pas leur temps à appliquer la formule sur un monome de degré 1 ou 0.
Quant à k, je t'avoue que je l'ai fait uniquement par rapport à elle afin de lui rendre l'explication la plus intelligible possible.

par **Archibald** » 11 Avr 2013, 09:36

juudu62 a écrit:donc a = -4 et b=2
Le coefficient directeur de la droite a est négatif donc tu j'en déduis que la fonction dérivée est décroissante : elle va du positif au négatif. Et elle doit change de signe en -b/a = -2/-4 (f'(0.5)=12.5) non ?

je peux alors construire le tableau de signe de la dérivée f' : elle est de signe + sur ]-infini,0.5[ et de signe - sur ]0.5,+infini[
Après avoir fait ce tableau, je peux en déduire le tableau de variation de f , qui est croissante là où sa dérivée est de signe + (donc sur ]-infini,0.5[) et décroissante là où sa dérivée est de signe - (donc sur ]0.5,+infini[0.5

c'est correcte ?

[CENTER]

[/CENTER]

Après, la formulation pourrait être plus rigoureuse mais je pense pas qu'on t'en tiendra compte en première.

Tu pourrais mettre une photo de tes tableaux de signe et de variation pour voir si tout est ok ?

par **juudu62** » 11 Avr 2013, 09:40

merci mais je pense que sa ira

par **Sylviel** » 11 Avr 2013, 10:03

@Archi : sur les conditions je ne sais pas trop si c'est une simplification ou pas. Si on n'écris rien les élèves ne se pose pas la question, donc je pense que c'est plus simple. Ils ne l'ont pas démontrer dans le cas général, ne savent même pas ce que c'est si n est non entier, mais ça reste vrai... Donc je suis plus partant pour ne pas donner de conditions du tout. Maintenant ce n'est qu'un avis pédagogique sans certitudes :zen:

par **juudu62** » 11 Avr 2013, 10:27

merci beaucoup mais j'aurais besoins d'aide pour les encadrement ( l'extremum je les deja fait )

par **Sylviel** » 11 Avr 2013, 10:34

tu peux les obtenirs en regardant ton tableau de variation. Tu auras juste besoin de calculer certaines valeurs de ta fonction.

Exemple :

si tu as une fonction f qui est croissante entre 0 et 3 et que tu veux un encadrement pour x entre 1 et 2, il suffit d'écrire :
1 < x < 2
donc puisque f est croissante
f(1)< f(x) < f(2).

Si f était décroissante il suffit d'inverser l'inégalité :
f(1) > f(x) > f(2).

Finalement si elle admet un extrêmum il faut faire un petit dessin et réfléchir 15 secondes :-)

par **juudu62** » 11 Avr 2013, 10:36

Sylviel a écrit:tu peux les obtenirs en regardant ton tableau de variation. Tu auras juste besoin de calculer certaines valeurs de ta fonction.

Exemple :

si tu as une fonction f qui est croissante entre 0 et 3 et que tu veux un encadrement pour x entre 1 et 2, il suffit d'écrire :
1 f(x) > f(2).

Finalement si elle admet un extrêmum il faut faire un petit dessin et réfléchir 15 secondes

merci beaucoup pour ton aide super cite ( en passant

)

F(x)=12

Qui est en ligne