Puissance/racine 0
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par eric_the_snake » 22 Mar 2013, 16:15
par eric_the_snake » 22 Mar 2013, 16:15
Bonjour,
J'ai une petite question qui me tracasse.
Si on pose :
3^3 = 27 ==>
racinecubique(3^3) = racinecubique(27) ==>
3 = racinecubique(27)
Pourquoi ne peut-on pas poser :
3^0 = 1 ==>
racinezero(3^0) = racinezero(1) ==>
3 = racinezero(1)
merci,
ETS

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 22 Mar 2013, 17:00
par chan79 » 22 Mar 2013, 17:00
eric_the_snake a écrit:Bonjour,
J'ai une petite question qui me tracasse.
Si on pose :
3^3 = 27 ==>
racinecubique(3^3) = racinecubique(27) ==>
3 = racinecubique(27)
Pourquoi ne peut-on pas poser :
3^0 = 1 ==>
racinezero(3^0) = racinezero(1) ==>
3 = racinezero(1)
merci,
ETS
dans

, l'exposant n'est pas 3
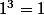
et on a bien

ou encore
^3=-1)
et on a bien


-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 22 Mar 2013, 17:02
par ampholyte » 22 Mar 2013, 17:02
Bonjour,
Il faut se souvenir que la racine n-ième peut s'écrire sous la forme

or pour n = 0, on a 1/0 qui n'est pas définit donc, tu ne peux pas définir la fonction

.
 par eric_the_snake » 25 Mar 2013, 16:13
par eric_the_snake » 25 Mar 2013, 16:13
Merci Ampholyte de ta réponse.
Mais dans ce cas, pourquoi pose-t-on a^0 = 1 ?
Si
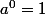
alors :
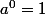
==>

Ce qui amène la même erreur.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 25 Mar 2013, 16:20
par ampholyte » 25 Mar 2013, 16:20
Attention :

Donc :

ou encore


On aurait plutôt :

Pour information, tu peux écrire également une puissance sous la forme suivante:
})
(forme exponentielle)
Cela répond donc à ta question
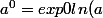} = e^0 = 1)
(par définition de la fonction exponentielle)
 par eric_the_snake » 25 Mar 2013, 16:26
par eric_the_snake » 25 Mar 2013, 16:26
Oui, effectivement, excuse mon erreur.
Merci,
ETS
 par eric_the_snake » 25 Mar 2013, 21:47
par eric_the_snake » 25 Mar 2013, 21:47
J'ai une dernière question

Si
^1)
donne -2
Pourquoi
^{1/2})
donne 2 considérant que
^b = x^{ab})
?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 26 Mar 2013, 00:35
par ampholyte » 26 Mar 2013, 00:35
Sauf que pour les exposants paires inverse il faut que le nombre soit positif.
^{1/2} = (-4)^{1/2} = \sqrt{-4})
n'est pas défini une racine carrée est toujours positif !
^{1/3} = \sqrt[3]{-4})
est défini !
Par contre :
^2)^{1/2} = (4)^{1/2} = \sqrt{4}= 2)
^2)^{1/2} = ((2)^{2})^{1/2} = 2^{2 * 1/2} = 2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 157 invités
