Bonjour,
J'ai un DM à faire pour demain
l'exercice se trouve dans ce lien :
http://maths.bro.free.fr/Files/dm3.pdf
c'est l'éxercice 2.
partie1:
1/a. 9*8=72 donc la somme vaut 72
b. (72²/8)-9² = 567
c. 72²
2/a. notes avec 10 controle fait 100
8 controles : 72
x9+x10=28
72+28=100
b. ecart type =3 donc la variance=3²=9
sigma²8+9²+9 =720
partie 2
1/ t+x10=28
t²+x10² < 400
t²=(28-x10)²
t²-28t<-192
t²-t<-192/28
donc c'est negatif
2/ soit delta le discriminant de cette fonction : 28²-4*1*192=16=4²
S= (12;16)
3/x9 peut etre compris entre 12 et 16
si x9=12 alors x10=16
13 15
14 14
15 13
16 12
partie 3 :
1/si k <20 et p<20
pour 4/ je sais pas....
Aidez-moi s'il vous plait. :we:
Statistique
10 messages
- Page 1 sur 1
par C.Ret » 11 Nov 2012, 17:33
Bonjour,
Pour l'excercice n°2 - partie 1 :
1/
a) OK
b) A quoi correspond l'expression de l'énoncé (ce n'est pas dit dans ton post) ?
A mon avis c'est une question du cours, et quelque chose d'important n'a pas été compris !
c) Je ne suis pas d'accord avec les résultats numériques b) et c).
2/
a) Bon OK pour x9+x10=28 (même si rédiger un peu plus rendrait les choses plus clair)
b) J'ai rien compris, comment arrives-tu à (x9)²+(x10)² <= 400 ?
Une variance de 3 fait 9 ??
Pour l'excercice n°2 - partie 2 :
1/
Il faut mieux rédiger, on ne comprends pas comment tu arrive au résultat.
Telle qu'elle est formulée, la réponse n'est pas valable, il faut montré que l'on arrive à une inéquation, je ne vois nulle part celle-ci. AU contraire tu arrive à une autre inéquation donc cela démontre que celle de l'énoncé est fausse ??
2/ OK
3/
Ca ce sont uniquement les couples de notes pour avoir au moins une moyenne de 10.
Mais n'y a-t-il pas des couples de notes possible qui donnent plus de 10 de moyenne tout en n'augmentant pas la variance de plus de 3 pts. ?
Partie 3.
1/
Euh! Quel est le but de cet algorithme ?
A mon avis c'est d'afficher tous les couples de note (x9,x10) qui permettront d'atteindre au moins 10 de moyenne sans augmenter la variancle des notes de plus de 3 pts.
En fait cet algorithme va permettre de vérifier les réponses de la partie 2.
En mettant les test que tu sugère, la machine va afficher 400 paires de notes :
(0,0)(0,1)(0,2)(0,3)...(0,19)(1,0)(1,1)(1,2)... ...(19,18)(19,19)
(J'ai la flèe de les recper toutes !)
2/
Le test est au centre de deux boucles imbriquées comptant de 0 à 20 (donc 21 éléments).
A ton avis, combien de fois la machine va effectuer ce test après avoir parcourru les deux boucles dans leur intégralité ?
3/
Tu as un système XCas près de toi ?
Bonus/
Facile !
Implémenter un compteur dans un algorithme c'est le b-a-b-a de l'informatique !
Pour l'excercice n°2 - partie 1 :
1/
a) OK
b) A quoi correspond l'expression de l'énoncé (ce n'est pas dit dans ton post) ?
A mon avis c'est une question du cours, et quelque chose d'important n'a pas été compris !
c) Je ne suis pas d'accord avec les résultats numériques b) et c).
2/
a) Bon OK pour x9+x10=28 (même si rédiger un peu plus rendrait les choses plus clair)
b) J'ai rien compris, comment arrives-tu à (x9)²+(x10)² <= 400 ?
Une variance de 3 fait 9 ??
Pour l'excercice n°2 - partie 2 :
1/
Il faut mieux rédiger, on ne comprends pas comment tu arrive au résultat.
Telle qu'elle est formulée, la réponse n'est pas valable, il faut montré que l'on arrive à une inéquation, je ne vois nulle part celle-ci. AU contraire tu arrive à une autre inéquation donc cela démontre que celle de l'énoncé est fausse ??
2/ OK
3/
Ca ce sont uniquement les couples de notes pour avoir au moins une moyenne de 10.
Mais n'y a-t-il pas des couples de notes possible qui donnent plus de 10 de moyenne tout en n'augmentant pas la variance de plus de 3 pts. ?
Partie 3.
1/
Euh! Quel est le but de cet algorithme ?
A mon avis c'est d'afficher tous les couples de note (x9,x10) qui permettront d'atteindre au moins 10 de moyenne sans augmenter la variancle des notes de plus de 3 pts.
En fait cet algorithme va permettre de vérifier les réponses de la partie 2.
En mettant les test que tu sugère, la machine va afficher 400 paires de notes :
(0,0)(0,1)(0,2)(0,3)...(0,19)(1,0)(1,1)(1,2)... ...(19,18)(19,19)
(J'ai la flèe de les recper toutes !)
2/
Le test est au centre de deux boucles imbriquées comptant de 0 à 20 (donc 21 éléments).
A ton avis, combien de fois la machine va effectuer ce test après avoir parcourru les deux boucles dans leur intégralité ?
3/
Tu as un système XCas près de toi ?
Bonus/
Facile !
Implémenter un compteur dans un algorithme c'est le b-a-b-a de l'informatique !
par trisha19 » 11 Nov 2012, 18:25
Partie1:
1/
b. cette expression correspond à la variance
puisque la somme vaut 72, je le met au carre . donc (72²/8)-9²
c. la somme vaut 72, je le met au carre
bah sinon, que dois-je écrire s'il vous plait pour b et c
b) Une variance de 3 fait 9 ?? : ecart type est de 3 (dans l'énoncé) variance = ecart type ²
sinon je sais pas
Partie 2 :
1/ On a : x9 = t et x10 = 28 - x9 = 28 - t.
On remplace ensuite x9 et x10 par leur valeur dans l'inéquation :
x9² + x10² <400
je sais pas si c'est bon, car je n'arrive pas encore a l'expression
Ou serais- ce la reponse à la 2/b de la partie 1
2/ d'accord
3/Ca ce sont uniquement les couples de notes pour avoir au moins une moyenne de 10.
Mais n'y a-t-il pas des couples de notes possible qui donnent plus de 10 de moyenne tout en n'augmentant pas la variance de plus de 3 pts. ?
Bah je sais pas trop ;ca verifie l'equation. auriez-vous d'autre couple ?
Partie 3 :
1/ oui ca permet de verifier lesd reponses de la partie 2
en faite c'est :
si k+p=28 et k²+p²<=400
et ben je retrouve les couples de solutions
"si x9=12 alors x10=16
13 15
14 14
15 13
16 12"
2/ je penserais à 40 fois
3/j'ai télécharger Xcas
en faite ca fera :
//k designe la note du 9ieme devoir
//p designe la note du 10ieme devoir
c:=0
pour k de 0 jusque 20 faire
pour p de 0 jusque 20 faire
si k +p<28 et k²+p²<=400
alors
c:=c+1
afficher (k,p)
afficher(c)
fsi;
fpour;
fpour;
Merci d'avance, c'est pour demain
1/
b. cette expression correspond à la variance
puisque la somme vaut 72, je le met au carre . donc (72²/8)-9²
c. la somme vaut 72, je le met au carre
bah sinon, que dois-je écrire s'il vous plait pour b et c
b) Une variance de 3 fait 9 ?? : ecart type est de 3 (dans l'énoncé) variance = ecart type ²
sinon je sais pas
Partie 2 :
1/ On a : x9 = t et x10 = 28 - x9 = 28 - t.
On remplace ensuite x9 et x10 par leur valeur dans l'inéquation :
x9² + x10² <400
je sais pas si c'est bon, car je n'arrive pas encore a l'expression
Ou serais- ce la reponse à la 2/b de la partie 1
2/ d'accord
3/Ca ce sont uniquement les couples de notes pour avoir au moins une moyenne de 10.
Mais n'y a-t-il pas des couples de notes possible qui donnent plus de 10 de moyenne tout en n'augmentant pas la variance de plus de 3 pts. ?
Bah je sais pas trop ;ca verifie l'equation. auriez-vous d'autre couple ?
Partie 3 :
1/ oui ca permet de verifier lesd reponses de la partie 2
en faite c'est :
si k+p=28 et k²+p²<=400
et ben je retrouve les couples de solutions
"si x9=12 alors x10=16
13 15
14 14
15 13
16 12"
2/ je penserais à 40 fois
3/j'ai télécharger Xcas
en faite ca fera :
//k designe la note du 9ieme devoir
//p designe la note du 10ieme devoir
c:=0
pour k de 0 jusque 20 faire
pour p de 0 jusque 20 faire
si k +p<28 et k²+p²<=400
alors
c:=c+1
afficher (k,p)
afficher(c)
fsi;
fpour;
fpour;
Merci d'avance, c'est pour demain
par C.Ret » 11 Nov 2012, 19:53
1/
b.cette expression correspond à la variance
OUI c'est bien la relation de König-Huygens.
Mais l'énoncé dit que l'écart-type est de trois, ce qui fait une variance de 9 (non ?)
Donc, si cette expression est la variance, pourquoi le résultat numérique ne fait pas 9 ?
puisque la somme vaut 72, je le mets au carre . donc (72²/8)-9²
Je crois qu'il y a confusion entre
, 
et ^2)
ex.:
^2 = (1 + 2 + 3)^2 = 6^2 = 36)
c. la somme vaut 72, je la mets au carré
D'après moi,
Ce qui fait bien une variance de 9, c'est à dire un écart type de 3.
b) Une variance de 3 fait 9 ?
Nous sommes donc d'accord, l'expression de la question b) est la variance et elle fait 9 et non 567 comme indiqué dans le premier post !
2/
a) OK. Pour atteindre 10, il faut que la somme des 10 notes fasse 100.
La somme des 8 premières notes fait 72, reste 28.
Donc effectivement x9+x10 = 28
b)
L'objectif est de ne pas augmenter la variance de plus de 3 pts.
La variance des huit premières notes est de 9, l'objectif est donc de ne pas dépasser 12.
On utilise à nouveau la relation de König-Huygens mais cette fois pour les 10 notes, une moyenne de 10/20 et une variance maximale de 12.
Or)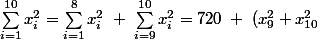
On obtient donc :
\time 10\,-\,720)
soit 
Partie 2 :
1/ On a : x9 = t et x10 = 28 - x9 = 28 - t.
On remplace ensuite x9 et x10 par leur valeur dans l'inéquation :
x9² + x10²<400
je sais pas si c'est bon, car je n'arrive pas encore a l'expression
Ou serait-ce la reponse à la 2/b de la partie 1
Si c'est bon, c'est moi qui confondais la question 1/ de la partie 2 avec la question 2 de la partie 1 ! :mur:
En substituant comme indiqué, je trouve
En divisant par deux, on obtient bien la relation qu'il fallait vérifiée:
2/ OK d'accord s'il te plait merci de rien.
3/Bah je sais pas trop ;ca verifie l'equation. auriez-vous d'autre couple ?
Bonne question.
Mais à bien y réflèchir, ces couples de notes vérifient en fait les deux objectifs, puisque nous avons utilisé pour construire l'inéquation les deux contraintes, celle concernant la moyenne à 10 (la somme qui fait 28) et celle concernant la variance (la somme des carrés inférieure ou égale à 400).
Donc,normalement, si nous ne nous sommes pas plantés, la partie 3 va confirmer qu'il y en a pas d'autres. ! :lol3:
Partie 3 :
1/ oui ca permet de verifier lesd reponses de la partie 2 en faite c'est :
si k+p=28 et k²+p²<=400
Très juste. excellant !
et ben je retrouve les couples de solutions
"si x9=12 alors x10=16
13 15
14 14
15 13
16 12"
2/ je penserais à 40 fois
Presque, le calcul est parait bon, mais de 0 à 20 cela fait 21 notes.
Chaque boucle "boucle" donc 21 fois, le test sera exécuté 21x21 = 441 fois.
3/j'ai télécharger Xcas
Moi, j'ai programmé mon HP-28S.
Mais XCas cela semmble bien. Je vais essayé aussi.
OK ! Excellant travail ! Et le bonus est gagné !
Petit détail, le compteur peut n'être affiché qu'à la fin.
Resultats:
b.cette expression correspond à la variance
OUI c'est bien la relation de König-Huygens.
Mais l'énoncé dit que l'écart-type est de trois, ce qui fait une variance de 9 (non ?)
Donc, si cette expression est la variance, pourquoi le résultat numérique ne fait pas 9 ?
puisque la somme vaut 72, je le mets au carre . donc (72²/8)-9²
Je crois qu'il y a confusion entre
ex.:
c. la somme vaut 72, je la mets au carré
D'après moi,
Ce qui fait bien une variance de 9, c'est à dire un écart type de 3.
b) Une variance de 3 fait 9 ?
Nous sommes donc d'accord, l'expression de la question b) est la variance et elle fait 9 et non 567 comme indiqué dans le premier post !
2/
a) OK. Pour atteindre 10, il faut que la somme des 10 notes fasse 100.
La somme des 8 premières notes fait 72, reste 28.
Donc effectivement x9+x10 = 28
b)
L'objectif est de ne pas augmenter la variance de plus de 3 pts.
La variance des huit premières notes est de 9, l'objectif est donc de ne pas dépasser 12.
On utilise à nouveau la relation de König-Huygens mais cette fois pour les 10 notes, une moyenne de 10/20 et une variance maximale de 12.
Or
On obtient donc :
Partie 2 :
1/ On a : x9 = t et x10 = 28 - x9 = 28 - t.
On remplace ensuite x9 et x10 par leur valeur dans l'inéquation :
x9² + x10²<400
je sais pas si c'est bon, car je n'arrive pas encore a l'expression
Ou serait-ce la reponse à la 2/b de la partie 1
Si c'est bon, c'est moi qui confondais la question 1/ de la partie 2 avec la question 2 de la partie 1 ! :mur:
En substituant comme indiqué, je trouve
En divisant par deux, on obtient bien la relation qu'il fallait vérifiée:
2/ OK d'accord s'il te plait merci de rien.
3/Bah je sais pas trop ;ca verifie l'equation. auriez-vous d'autre couple ?
Bonne question.
Mais à bien y réflèchir, ces couples de notes vérifient en fait les deux objectifs, puisque nous avons utilisé pour construire l'inéquation les deux contraintes, celle concernant la moyenne à 10 (la somme qui fait 28) et celle concernant la variance (la somme des carrés inférieure ou égale à 400).
Donc,normalement, si nous ne nous sommes pas plantés, la partie 3 va confirmer qu'il y en a pas d'autres. ! :lol3:
Partie 3 :
1/ oui ca permet de verifier lesd reponses de la partie 2 en faite c'est :
si k+p=28 et k²+p²<=400
Très juste. excellant !
et ben je retrouve les couples de solutions
"si x9=12 alors x10=16
13 15
14 14
15 13
16 12"
2/ je penserais à 40 fois
Presque, le calcul est parait bon, mais de 0 à 20 cela fait 21 notes.
Chaque boucle "boucle" donc 21 fois, le test sera exécuté 21x21 = 441 fois.
3/j'ai télécharger Xcas
Moi, j'ai programmé mon HP-28S.
Mais XCas cela semmble bien. Je vais essayé aussi.
- Code: Tout sélectionner
[COLOR=Blue]
//k designe la note du 9ieme devoir
//p designe la note du 10ieme devoir[/COLOR]
// c compte les couples de note possibles
[COLOR=Blue]c:=0
pour k de 0 jusque 20 faire
pour p de 0 jusque 20 faire
si (k+p=28) et (k²+p²<=400)
alors
c:=c+1
afficher (k,p)
fsi;
fpour;
fpour;[/COLOR]
[B]afficher c;[/B]
// ----------------------
OK ! Excellant travail ! Et le bonus est gagné !
Petit détail, le compteur peut n'être affiché qu'à la fin.
Resultats:
- Code: Tout sélectionner
(12,16) (13,15) (14,14) (15,13) (16,12) 5
par trisha19 » 11 Nov 2012, 20:09
1/
b.cette expression correspond à la variance
OUI c'est bien la relation de König-Huygens.
Mais l'énoncé dit que l'écart-type est de trois, ce qui fait une variance de 9 (non ?)
Donc, si cette expression est la variance, pourquoi le résultat numérique ne fait pas 9 ?
Tres bonne question !
Dans les exemples que vous m'adit dit ne serais-ce pas le 2ème ?Parce que si c'est ca, je trouve 1+4+9+16+25+36+49+64=204 ??
et si c'est la troisieme = (1+2+3+4+5+6+7+8)² =54²
b.cette expression correspond à la variance
OUI c'est bien la relation de König-Huygens.
Mais l'énoncé dit que l'écart-type est de trois, ce qui fait une variance de 9 (non ?)
Donc, si cette expression est la variance, pourquoi le résultat numérique ne fait pas 9 ?
Tres bonne question !
Dans les exemples que vous m'adit dit ne serais-ce pas le 2ème ?Parce que si c'est ca, je trouve 1+4+9+16+25+36+49+64=204 ??
et si c'est la troisieme = (1+2+3+4+5+6+7+8)² =54²
par C.Ret » 11 Nov 2012, 20:40
J'ai corrigé mon post (j'avais mis i au lieu de x). Désolé.
Dans l'excercice les notes sont notées
pour i allant de 1 à 8 ou 10.
Dans mes trois petits exemples, le x (ou le i) ne correspond pas du tout aux onnées de l'excercice :
 + ... + (b-1) + b)
Je voulais juste montré qu'en général, la somme des carrés n'est pas égale au carré de la somme. :lol3:
Dans l'excercice les notes sont notées
Dans mes trois petits exemples, le x (ou le i) ne correspond pas du tout aux onnées de l'excercice :
Je voulais juste montré qu'en général, la somme des carrés n'est pas égale au carré de la somme. :lol3:
par trisha19 » 11 Nov 2012, 21:47
j'ai tapé tout ca comme vous me l'avez écrit mais je n'arrive pas trouver le meme resultat que vous.
pour c, ca me fait "recursive definition" ou pleins, pleins de chiffres.
j'ai pas tapé :
"// ----------------------
[/COLOR]" est-ce vraiment necessaire, de toute facon, ca me fait un truc bizarre aussi
je peux pas mettre
afficher c; comme cela; je dois ecrire afficher(c);
auriez-vous une idée de pourquoi ca ne marche pas...
Sinon avez-vous deja imprimer sur Xcas; est-ce que ca on voit seulement les 2 petits cadres que vous avez marquez ?
Parce que je dois l'imprimer et le montrer au professeur.
//k designe la note du 9ieme devoir
//p designe la note du 10ieme devoir
// c compte les couples de note possibles
c:=0
pour k de 0 jusque 20 faire
pour p de 0 jusque 20 faire
si (k+p<28) et (k²+p²<=400)
alors
c:=c+1
afficher (k,p)
fsi;
fpour;
fpour;
afficher c;
pour c, ca me fait "recursive definition" ou pleins, pleins de chiffres.
j'ai pas tapé :
"// ----------------------
[/COLOR]" est-ce vraiment necessaire, de toute facon, ca me fait un truc bizarre aussi
je peux pas mettre
afficher c; comme cela; je dois ecrire afficher(c);
auriez-vous une idée de pourquoi ca ne marche pas...
Sinon avez-vous deja imprimer sur Xcas; est-ce que ca on voit seulement les 2 petits cadres que vous avez marquez ?
Parce que je dois l'imprimer et le montrer au professeur.
//k designe la note du 9ieme devoir
//p designe la note du 10ieme devoir
// c compte les couples de note possibles
c:=0
pour k de 0 jusque 20 faire
pour p de 0 jusque 20 faire
si (k+p<28) et (k²+p²<=400)
alors
c:=c+1
afficher (k,p)
fsi;
fpour;
fpour;
afficher c;
par C.Ret » 11 Nov 2012, 21:55
Je ne connais pas Xcas, il faut que je me renseigne.
A mon avis, si afficer(c), affiche la valeur de c, alors la syntaxe afficher (k,p) n'est pas bonne.
...
A mon avis, si afficer(c), affiche la valeur de c, alors la syntaxe afficher (k,p) n'est pas bonne.
...
par trisha19 » 11 Nov 2012, 22:09
C.Ret a écrit:Je ne connais pas Xcas, il faut que je me renseigne.
A mon avis, si afficer(c), affiche la valeur de c, alors la syntaxe afficher (k,p) n'est pas bonne.
...
auriez-vous la possibilité de vous renseigner pour demain matin (avant 12h) s'il vous plait?
par C.Ret » 11 Nov 2012, 22:36
Je viens d'utiliser et créer mon premier programme sous l'environnement Xcas (c'est très moche - je préfère de loin utiliser mon HP-28S ou mon Commodore C128D).
Je n'ai rencontré aucun problème particulier :
Affiche :
Sans aucun soucis.
Je n'ai rencontré aucun problème particulier :
- Code: Tout sélectionner
[COLOR=YellowGreen]// k designe la note du 9ieme devoir
// p designe la note du 10ieme devoir
// c compte les couples de note possibles
// t compte le nombre de foi que le test est fait[/COLOR]
c:=0;
t:=0;
[COLOR=RoyalBlue]pour[/COLOR] k [COLOR=RoyalBlue]de[/COLOR] 0 [COLOR=RoyalBlue]jusque[/COLOR] 20 [COLOR=RoyalBlue]faire[/COLOR]
[COLOR=RoyalBlue]pour[/COLOR] p [COLOR=RoyalBlue]de[/COLOR] 0 [COLOR=RoyalBlue]jusque[/COLOR] 20 [COLOR=RoyalBlue]faire[/COLOR]
t:=t+1;
[COLOR=RoyalBlue]si[/COLOR] (k+p=28) [COLOR=RoyalBlue]et[/COLOR] (k²+p²<=400) [COLOR=RoyalBlue]alors[/COLOR]
c:=c+1;
[COLOR=DarkRed]afficher[/COLOR](k,p)
[COLOR=RoyalBlue]fsi[/COLOR];
[COLOR=RoyalBlue]fpour[/COLOR];
[COLOR=RoyalBlue]fpour[/COLOR];
[COLOR=DarkRed]afficher[/COLOR](c);
[COLOR=DarkRed]afficher[/COLOR](t);
[COLOR=YellowGreen]// ------------------------------------------[/COLOR]
Affiche :
- Code: Tout sélectionner
12,16
13,15
14,14
15,13
16,12
c:5
t:441
Sans aucun soucis.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :