Aide pour un exercice svp
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 13:57
par mrpopo » 11 Nov 2012, 13:57
Bonjour , j'ai besoin d'aide pour un exercice, voilà l'énoncé :
On considère la fonction g : x -->f(x) = 1/x définie sur l'intervalle ]-;);0[U]0;+;)[
b) Démontrer que g est strictement décroissante sur ]-;);0[.
J'ai donc pris au hasard les chiffres -1 et -2
1
_ = -1
-1
1
_ = -0,5
-2
-1 est plus grand que -0,5 ou l'inverse ? g est donc strictement décroissante sur ]-;);0[ ? merci d'avance
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 11 Nov 2012, 14:13
par Dlzlogic » 11 Nov 2012, 14:13
Bonjour,
Il me semble qu'on vous demande de le démontrer. Un vague vérification n'a aucune valeur.
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 15:34
par mrpopo » 11 Nov 2012, 15:34
Dlzlogic a écrit:Bonjour,
Il me semble qu'on vous demande de le démontrer. Un vague vérification n'a aucune valeur.
C'est par cette vérification que je veux le démontrer. Si c'est valable pour ces chiffres , ça l'est pour tous les chiffres compris dans ]-;);0[, et c'est ce que je veux expliquer.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 15:39
par mcar0nd » 11 Nov 2012, 15:39
mrpopo a écrit:C'est par cette vérification que je veux le démontrer. Si c'est valable pour ces chiffres , ça l'est pour tous les chiffres compris dans ]-;);0[, et c'est ce que je veux expliquer.
Bonjour à vous deux,
Tu ne peux pas faire comme ça pour une démonstration, comme te l'a dit Dlzlogic, tu dois le faire pour
n'importe quel nombre de ton intervalle.
Tu n'as pas le droit de donner de valeurs pour faire ta démonstration.
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 15:48
par mrpopo » 11 Nov 2012, 15:48
mcar0nd a écrit:Bonjour à vous deux,
Tu ne peux pas faire comme ça pour une démonstration, comme te l'a dit Dlzlogic, tu dois le faire pour n'importe quel nombre de ton intervalle.
Tu n'as pas le droit de donner de valeurs pour faire ta démonstration.
Alors comment faire svp ? C'est la seule façon que j'ai trouvée :-/
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 15:53
par mcar0nd » 11 Nov 2012, 15:53
mrpopo a écrit:Alors comment faire svp ? C'est la seule façon que j'ai trouvée :-/
Prend deux réels,

et

tels que

.
Et comment tu pourrais faire?
Tu pourrais comparer
)
et
)
en faisant leur différence.

-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 15:57
par mrpopo » 11 Nov 2012, 15:57
mcar0nd a écrit:Prend deux réels,

et

tels que

.
Et comment tu pourrais faire?
Tu pourrais comparer
)
et
)
en faisant leur différence.

En faisant leur difference? Comment ça ? Excuse moi, je ne suis pas très doué pour les maths. ^^
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 16:00
par mcar0nd » 11 Nov 2012, 16:00
mrpopo a écrit:En faisant leur difference? Comment ça ? Excuse moi, je ne suis pas très doué pour les maths. ^^
Si ta fonction est décroissante, elle inverse le sens de l'inégalité.
En maths, étudier une différence, est une méthode pour prouver la décroissance (ou non d'ailleurs) d'une fonction.
 -f(x_2))
, ça te donne quoi?
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 11 Nov 2012, 16:01
par Dlzlogic » 11 Nov 2012, 16:01
Si j'ai une valeur x1, j'aurai une valeur y1 = f(x1)
même chose pour une valeur x2
Je fais la différence x2-x1, puis la différence y2-y1 et je regarde le résultat.
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 16:21
par mrpopo » 11 Nov 2012, 16:21
mcar0nd a écrit:Si ta fonction est décroissante, elle inverse le sens de l'inégalité.
En maths, étudier une différence, est une méthode pour prouver la décroissance (ou non d'ailleurs) d'une fonction.
 -f(x_2))
, ça te donne quoi?
ça donne f(x-1) ? :-/
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 16:28
par mcar0nd » 11 Nov 2012, 16:28
mrpopo a écrit:ça donne f(x-1) ? :-/
Non,
= \frac{1}{x_1})
et
= \frac{1}{x_2})
donc
-f(x_2)=...)
.
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 16:38
par mrpopo » 11 Nov 2012, 16:38
Je ne comprends pas, vraiment désolé je vois que tu essaies de me faire comprendre et raisonner mais je ne vois pas comment faire pour calculer ça.
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 16:39
par mcar0nd » 11 Nov 2012, 16:39
mrpopo a écrit:Je ne comprends pas, vraiment désolé je vois que tu essaies de me faire comprendre et raisonner mais je ne vois pas comment faire pour calculer ça.
Donc
 - f(x_2) = \frac{1}{x_1} - \frac{1}{x_2})
et si tu mets ça au même dénominateur, tu as quoi?
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 11 Nov 2012, 16:42
par Dlzlogic » 11 Nov 2012, 16:42
mrpopo a écrit:Je ne comprends pas, vraiment désolé je vois que tu essaies de me faire comprendre et raisonner mais je ne vois pas comment faire pour calculer ça.
Mais à cette étape il n'y a rien à faire juste à écrire au bout de la ligne ce qui est écrit au début de cette même ligne.
Le calcul viendra après.
PS, j'ai été trop lent, ou McarOn trop rapide.
Par contre, ce qui me semble sûr est que notre ami attend la réponse.
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 16:56
par mrpopo » 11 Nov 2012, 16:56
mcar0nd a écrit:Donc
 - f(x_2) = \frac{1}{x_1} - \frac{1}{x_2})
et si tu mets ça au même dénominateur, tu as quoi?
Après avoir mis au même dénominateur j'obtiens
 - (x_1))
____________
)
²
-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 16:57
par mrpopo » 11 Nov 2012, 16:57
Dlzlogic a écrit:Mais à cette étape il n'y a rien à faire juste à écrire au bout de la ligne ce qui est écrit au début de cette même ligne.
Le calcul viendra après.
PS, j'ai été trop lent, ou McarOn trop rapide.
Par contre, ce qui me semble sûr est que notre ami attend la réponse.
Je n'attends pas la réponse loin de là , mais je n'y arrive simplement pas, je ne comprends pas. :triste:
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 17:12
par mcar0nd » 11 Nov 2012, 17:12
mrpopo a écrit:Après avoir mis au même dénominateur j'obtiens
 - (x_1))
____________
)
²
Le dénominateur ne doit pas être au carré, c'est faux si tu le mets au carré.
Donc maintenant étudie le signe
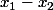
; celui de

et déduis en celui de ton quotient.

@Dlzlogic non, je ne pense pas qu'il (ou elle) attende la réponse sinon il (ou elle) n'essaierai pas de réfléchir.

-
mrpopo
- Messages: 9
- Enregistré le: 09 Nov 2012, 14:06
-
 par mrpopo » 11 Nov 2012, 17:17
par mrpopo » 11 Nov 2012, 17:17
Ah, je pense avoir trouvé comment faire en farfouillant dans mon livre, oui j'avais complètement faux. Un grand merci à vous deux, et merci beaucoup mcar0nd ! ^^
-
mcar0nd
- Membre Irrationnel
- Messages: 1929
- Enregistré le: 03 Mai 2012, 16:24
-
 par mcar0nd » 11 Nov 2012, 17:21
par mcar0nd » 11 Nov 2012, 17:21
mrpopo a écrit:Ah, je pense avoir trouvé comment faire en farfouillant dans mon livre, oui j'avais complètement faux. Un grand merci à vous deux, et merci beaucoup mcar0nd ! ^^
Normalement, tu dois trouver que ton quotient est positif.

De rien.

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 183 invités
²
