Z/pZ

[ev85]

Bonjour à tous,

Merci de m'aider pour cet exo :

Soit p un entier irreductible ou premier.

1) Montrer que Z/pZ est un corps

2) Quel est l'inverse de classe de 8 dans Z/11Z ?

3) Quel est l'inverse de classe de 25 dans Z/61Z ?

Alors ;

1) On a un theoreme qui dit que classe de x appartient à Z/pZ si et seulement si pgcd(x,p) = 1

Donc p premier => pour tout a dans { 1 ... p -1 } pgcd(a,p) = 1

D'apres le theoreme, a est inversible alors Z/pZ est un corps.

pour 2)3) ce qui me perturbe est que (Z/nZ, +, * ) est un anneau commutatif donc je ne sais pas avec quel loi cherché les inverses .


Merci beaucoup

Pour 2) et 3) Bézout est ton ami.

[zork]

pour l'inverse de 8 dans Z/11Z, on peut utiliser l'algo d'euclide
on trouve -4

[Manny06]

Bonjour à tous,

Merci de m'aider pour cet exo :

Soit p un entier irreductible ou premier.

1) Montrer que Z/pZ est un corps

2) Quel est l'inverse de classe de 8 dans Z/11Z ?

3) Quel est l'inverse de classe de 25 dans Z/61Z ?

Alors ;

1) On a un theoreme qui dit que classe de x appartient à Z/pZ si et seulement si pgcd(x,p) = 1

Donc p premier => pour tout a dans { 1 ... p -1 } pgcd(a,p) = 1

D'apres le theoreme, a est inversible alors Z/pZ est un corps.

pour 2)3) ce qui me perturbe est que (Z/nZ, +, * ) est un anneau commutatif donc je ne sais pas avec quel loi cherché les inverses .


Merci beaucoup

il s'agit de l'inverse pour la loi *

[Nightmare]

1) On a un theoreme qui dit que classe de x appartient à Z/pZ si et seulement si pgcd(x,p) = 1

Tu voulais dire "classe de x est inversible dans Z/pZ si et ssi pgcd(x,p)=1 non?

[Nightmare]

Dans un anneau, quand on parle d'inverse, c'est pour la loi multiplicative, sinon, on parle de symétrique.

Cela étant, chercher les symétriques dans Z/pZ n'a pas grand intérêt : Le symétrique de x, c'est -x, ou encore p-x.

[Luc]

Bonjour Méliemélo,

Déjà Z/pZ est un corps si p est premier, donc il y a une solution unique modulo p à l'équation ax=1 d'inconnue x.
Ensuite,
dans Z/11Z, pas 1.
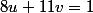
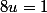
Pour trouver l'inverse de 8, il suffit d'utiliser une relation de Bézout entre 11 et 8 (ils sont premiers entre eux). En effet, si tu as dans Z, alors tu as dans Z/11Z. Pour trouver une relation de Bézout, soit tu la trouves de tête, soit tu fais l'algorithme de division d'Euclide jusqu'à trouver 1, puis tu remplaces les restes de proche en proche.

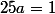
Pour dans Z/61Z, c'est exactement la même méthode.

Luc

[Nightmare]

La méthode de Luc qui est d'appliquer Bézout est la plus "viable" car applicable dans un Z/nZ où n n'est pas premier.

Cependant, pour Z/pZ, on a une méthode très rapide qui est donnée par le petit théorème de Fermat qui s'énoncé comme suit :

Si p est premier et a différent de p, alors .

Ainsi, l'inverse de a, c'est . Evidemment, le calcul de a^(p-2) peut être parfois laborieux.

Cela dit, cette méthode se généralise aussi à Z/nZ avec n non premier en utilisant le théorème d'Euler, mais je pense qu'à ce moment là il vaut mieux revenir à Bezout.

[Luc]

Oui le petit théorème de Fermat est très utile, en pratique on écrit p-2 en base 2 pour calculer avec un minimum d'opérations (exponentiation rapide). Je pense que cette méthode est bien meilleure que Bézout en terme de nombre d'opérations si p est un "grand" nombre premier, on ne fait que A*log(p) opérations. Quelqu'un connait la complexité moyenne de l'algorithme d'Euclide étendu avec Bézout?

Luc

[Nightmare]

De mémoire, je crois bien que l'algorithme d'Euclide étendu est aussi du k.log(n) !

[Nightmare]

Les liens internet semblent le confirmer.

[Luc]

Oui j'ai regardé http://www.labri.fr/perso/betrema/deug/poly/euclide.html qui est très bien et en fait j'ai l'impression que la complexité de l'algo d'Euclide étendu est la même (à une constante près) que celui du pgcd. Et celle-ci est majorée par le cas le plus défavorable , si a et b sont deux termes consécutifs de la suite de Fibonacci (il n'y aurait que des "1" en quotient), qui est exponentiel, d'où le résultat de la complexité logarithmique.