N^3 >= n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
capa57
- Membre Naturel
- Messages: 16
- Enregistré le: 02 Mar 2012, 17:02
-
 par capa57 » 02 Mar 2012, 18:21
par capa57 » 02 Mar 2012, 18:21
Prove or disprove that n^3 >= n given that n is an integer.
Je dois prouver que n au cube est supérieur ou égal à n , sachant que n est un entier
mais je vois pas ce qu'il y a à prouver... on le sait directement que c'est supérieur...
comment prouver cela ?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 02 Mar 2012, 18:33
par Euler07 » 02 Mar 2012, 18:33
Abon ?
-8 est plus grand que -2 ?
:livre:
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Mar 2012, 18:35
par globule rouge » 02 Mar 2012, 18:35
capa57 a écrit:Prove or disprove that n^3 >= n given that n is an integer.
Je dois prouver que n au cube est supérieur ou égal à n , sachant que n est un entier
mais je vois pas ce qu'il y a à prouver... on le sait directement que c'est supérieur...
comment prouver cela ?
Salut =)
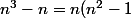 \geq 0)
donc...
Julie

-
capa57
- Membre Naturel
- Messages: 16
- Enregistré le: 02 Mar 2012, 17:02
-
 par capa57 » 02 Mar 2012, 18:38
par capa57 » 02 Mar 2012, 18:38
globule rouge a écrit:Salut =)
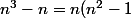 \geq 0)
donc...
Julie

pourquoi on cherche à faire -n ?
-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 02 Mar 2012, 18:39
par Elerinna » 02 Mar 2012, 18:39
Excepté l'étude de signe par factorisation triviale, quel est le contenu exhaustif du problème (en Anglais)? :)
-
capa57
- Membre Naturel
- Messages: 16
- Enregistré le: 02 Mar 2012, 17:02
-
 par capa57 » 02 Mar 2012, 18:42
par capa57 » 02 Mar 2012, 18:42
Elerinna a écrit:Excepté l'étude de signe par factorisation triviale, quel est le contenu exhaustif du problème (en Anglais)?

hum j'ai juste cette question : Prove or disprove that n^3 >= n given that n is an integer.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 02 Mar 2012, 19:20
par Le_chat » 02 Mar 2012, 19:20
Salut. Oui c'est evident, donc du coup les démonstrations de ce résultat paraissent un peu con:
Par exemple: Si n=0, c'est vrai, et si n;)1, n^2;)1 et en multipliant par n, n^3;)n.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mar 2012, 19:33
par Judoboy » 02 Mar 2012, 19:33
C'est un problème encore ouvert aujourd'hui ; apparemment ça serait indécidable. En tout cas je m'aventurerai pas là-dedans.
Ok je sors...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
