Limites1s
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
yahumi
- Membre Relatif
- Messages: 149
- Enregistré le: 19 Nov 2011, 13:39
-
 par yahumi » 14 Fév 2012, 23:17
par yahumi » 14 Fév 2012, 23:17
salut un aide pour cette limite lim(xtend vers pisur3) (2cosx-1 ) sur (3x-pi)
-
ksavier
- Membre Naturel
- Messages: 48
- Enregistré le: 13 Fév 2012, 20:06
-
 par ksavier » 15 Fév 2012, 01:18
par ksavier » 15 Fév 2012, 01:18
yahumi a écrit:salut un aide pour cette limite lim(xtend vers pisur3) (2cosx-1 ) sur (3x-pi)
Elle se calcule traditionnellement avec le changement de variable X=3x-pi,
c'est à dire x=(X+pi)/3=X/3+pi/3. qui ramène la limite à X tend vers 0 (c'est toujours plus facile)
Puis on utilise cos(a+b)=cos(a)cos(b) - ... (formulaire)
Et on utilise le fait qu'en 0 (voilà pourquoi c'est plus facile) on connaît les limites de (cos(t)-1)/t et celle de sin(t)/t (et ici un autre changement de variable t=X/3)
-
st00pid_n00b
- Membre Relatif
- Messages: 251
- Enregistré le: 03 Fév 2012, 19:54
-
 par st00pid_n00b » 15 Fév 2012, 06:12
par st00pid_n00b » 15 Fév 2012, 06:12
La méthode de ksavier me semble faire appel à des notions de terminale.
En 1ère S, tu viens probablement d'étudier les dérivées comme limite de taux de variation. Et ta limite ressemble fortement à un taux de variation, il suffit de factoriser par 2/3.
 - 1}{3x - \pi} = \frac23 \times \frac{cos(x) - \frac12}{x - \frac\pi3} = \frac23 \times \frac{cos(x) - cos(\frac\pi3)}{x - \frac\pi3})
Je pense que tu peux finir à partir de là

-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 15 Fév 2012, 06:38
par geegee » 15 Fév 2012, 06:38
yahumi a écrit:salut un aide pour cette limite lim(xtend vers pisur3) (2cosx-1 ) sur (3x-pi)
Bonjou r ,
règle de l'Hopital :
lim(x->pi/3)(-2sin(x))/3 = - racine3/3
-
yahumi
- Membre Relatif
- Messages: 149
- Enregistré le: 19 Nov 2011, 13:39
-
 par yahumi » 15 Fév 2012, 14:47
par yahumi » 15 Fév 2012, 14:47
et pour cette limite lim(x tend vers 0+)( racine tan x-racinetan2x)sur (tan3Xsur tan4x)
-
ksavier
- Membre Naturel
- Messages: 48
- Enregistré le: 13 Fév 2012, 20:06
-
 par ksavier » 15 Fév 2012, 21:50
par ksavier » 15 Fév 2012, 21:50
yahumi a écrit:et pour cette limite lim(x tend vers 0+)( racine tan x-racinetan2x)sur (tan3Xsur tan4x)
il suffit de démontrer que le (tan3Xsur tan4x) tend vers 3/4
Le numérateur tend lui vers 0.
indication :
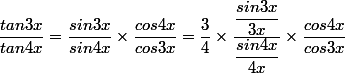
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
