Formes a + bi

[naruto-next]

salut,

il faut mettre sous la forme a +bi , le nombre complexe z tel que le module de z est 3 et argument -pi / 8

le -pi /8 me rebute

[romani01]

Salut.
Tu peux utiliser la formule de duplication .Tu remplaces
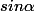
.Pour trouver ensuite tu utilises la relation
fondamentale sin²x+cos²x=1.

[rabihaudi]

salut,

il faut mettre sous la forme a +bi , le nombre complexe z tel que le module de z est 3 et argument -pi / 8

le -pi /8 me rebute

ecrire z comme z=3[cos(-pi/8)+isin(-pi/8)]
pour chercher cos(pi/8) utiliser la formule cos(2x)=2cos^2(x) - 1 et applique sur x=pi/8 ...

[naruto-next]

Merci mais je comprend pas . car je ne connais pas cos ( -pi / 8 ) , la formule ne m'aide pas puisque pour x = -pi / 8 ca me donne cos ( 2x ) = cos ( -pi / 4 ) mais moi je veux connaitre cos ( pi / 8 )

[annick]

Bonjour,
comme il t'a été dit : cos2x=2cos²x-1
Ici, x=-pi/8, donc 2x=-pi/4,

ce qui donne cos(-pi/4)=2cos²(-pi/8)-1

Tu connais cos(-pi/4), donc tu peux en déduire cos²(-pi/8)