1=2

par **Julien S.** » 28 Mai 2006, 12:47

Bonjour!

Juste pour le fun... une petite preuve, assez fine faut le dire (elle n'utilise pas de division par zéro) que 1=2 qu'un ami m'a montrée. Trouverez-vous l'erreur (moi j'ai quand même mis un petit moment pour la trouver).

On considère l'égalité (évidemment vraie):

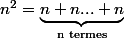
et on dérive les deux membres par rapport à n, ce qui donne:

donc

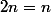
prenons

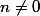
et simplifions par n, il vient:

2=1. :mur:

Je vous l'accorde, le "truc" n'est pas très fin, mais c'est joli non? :marteau:

par **Zebulon** » 28 Mai 2006, 12:57

Bonjour,
comment passe-vous de n² à 2n en divisant par n??

par **bluefog** » 28 Mai 2006, 13:39

on ne peut pas dériver par rapport à n car elle est considérée ici comme une variable entière et dans la définition de la dérivée, n est une variable REELLE.

par **serge75** » 28 Mai 2006, 13:40

deux erreurs : un ta formule n'est valide que pour n entier, et donc pas de dérivation envisageable.
De plus, même en passant outre cette première erreur, ta somme n'est pas de taille constante, donc la formule de dérivation de la somme n'est pas valide.
voili voilà ! :we:

par **abel** » 28 Mai 2006, 17:00

J'en ai une dans le style.
1=(-1)²
or 1 = 1^(1/2) donc :
1=((-1)²)^(1/2)=(-1)^(2*1/2)=(-1)^1=-1 :
donc -1=1

par **Zebulon** » 28 Mai 2006, 17:12

Celle-là je la connais. Je crois que le problème est que

seulement pour a et b entiers.

par **rene38** » 28 Mai 2006, 18:30

Bonjour

Pour

et

réels,

Or la fonction ln n'est définie que sur

donc ...

par **meo** » 28 Mai 2006, 18:32

((-1)²)^1/2 = |-1| = 1
:briques:

1=2

1=2

Qui est en ligne