Aidez moi svp (DM)

[loumio]

Bonjour, voilà je suis en terminal s et j'ai un exercice dans mon DM que je n'y arrive pas.

L'exercice est:

Soit f la fonction définie sur R par: f(t) = te^(-2t+1)

1) Donnez le tableau de variation de f

2) résoudre f(t) = t

3) Soit (Un)n;)N la suite définie par : Un+1 = f(Un) et U0 = 1/4

a) Démontrez que U1 = 1/(4;)e)
b) Démontrez par récurrence que ;)n;)N, on a : 0 ;) Un ;) Un+1 ;) 1/2
c) Quelle semble être la limite de la suite (Un)n;)N

Merci de votre aide :we:

[Pixis]

Qu'as tu essayé, voire réussi à faire ?

[loumio]

J'ai essayé de faire le tableau de variation de f j'ai trouvé la dérivé f'(t) = te
et à l'équation j'ai juste trouvé te^(-2t+1) = t après je suis bloqué
puis la question 3 je suis complétement bloqué.

[Pixis]

Bon, déjà ta dérivée est fausse.
tu as
C'est sous la forme u*v avec


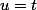
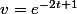
Quelle est la forme de la dérivée de u*v ?
Quelle est la dérivée de u ? Celle de v ?

[loumio]

la forme de la dérivée de u*v est u'v+uv'
u' = 1
v' = e^(-2)

[Pixis]

ok pour la dérivée de u*v et celle de u

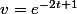
Mais celle de , c'est pas ça.
v est une fonction composée :
Elle est composée de la fonction

et

donc on a
v(t)=g o h (t)
c'est à dire

Et dans ce cas, la dérivée de v est :

Donc ici

d'où

Donc

A toi de continuer

[Fantomete]

Revois la formule de la dérivation de l'exponentielle car ce n'est pas ça.

[Pixis]

ok pour la dérivée de u*v et celle de u

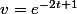
Mais celle de , c'est pas ça.
v est une fonction composée :
Elle est composée de la fonction

et

donc on a
v(t)=g o h (t)
c'est à dire

Et dans ce cas, la dérivée de v est :

Donc ici

d'où

Donc

A toi de continuer

[loumio]

Merci mais je n'y arrive pas aux deux autres questions. :help:

[Pixis]

2) résoudre f(t) = t

As-tu cherché ?
donc
Tu dois savoir résoudre ça non ? (attention à qui peut être nul ou pas ...)

a) Démontrez que U1 = 1/(4;)e)

La je pense que tu peux trouver tout seul, en lisant bien l'énoncé

b) Démontrez par récurrence que n;)N, on a : 0 Un Un+1 1/2

Connais-tu la méthode d'une récurrence ?

c) Quelle semble être la limite de la suite (Un)n;)N

On verra ça après

[loumio]

Pour la 3)a):
j'ai commencé par : U1 = 1/4.e^(-2.1/4+1) = 1/4(e^(2.1/4+1)) = 1/4e^3/2 et là je suis bloquer
Pour la 3)b):
J'ai trouvé :
Initialisation :
Pour n0 = 0 on a bien 0 1/4 1/4;)e 1/2
Hérédité :
Supposons qu'il existe n0 N tel que 0 UN UN+1 1/2
Cela implique t-il 0 UN+1 UN+2 1/2 ?
et là je bloque

[Pixis]

1/4.e^(-2.1/4+1) = 1/4(e^(2.1/4+1))

Où diantre est bien passé ce - ?

Si tu veux écrire :

alors il y a une petite erreur de calcul lors du passage à l'inverse de l'exponentielle