Bonjour à tous,
Je cherche à calculer les coordonnées d'une ligne parallèle à une autre en 2D. Sur un segment de deux points je sais faire mais sur une polyligne, c'est plus dur ...
En entrée j'ai une polyligne quelconque de n points (A, B, C, D) par exemple de coordonnées Ax, Ay, Bx, By ... et les points que je cherche à calculer (Ag, Bg, Cg, Dg) sont à une distance D.
Pour info c'est pour un logiciel de dessin, l'utilisateur saisit la ligne centrale d'un mur (vu de dessus) et je dois dessiner le mur avec son epaisseur et les angles entre deux murs successifs peuvent être quelconques.
Merci par avance.
Calcul de polylignes parallèles
7 messages
- Page 1 sur 1
salut,
mettons donc tes points A,B,C,D qui forment ta polyligne.
donc on s'interesse que à A B et C.
On va appeler A',B',C' la nouvelle polyligne.
On a (A'B')//(AB) ET (B'C')//(BC) avec d((A'B'), (AB))=d((B'C'), (BC))=e (ou d((ST),(UV)) représente la distance entre la droite (ST) et la droite (UV).
Pour le point A', en supposant qu'on a un angle du mur au bout orthogonal (donc BAA' = 90), on se place sur [AB] avec un point K.
et on écrit AK=e, pis on fait rotater le point K de -90° pour avoir notre point A'=K'.
donc les cordo de K sont données par la relation
d'ou
ensuite, on rotate K par rapport à l'origine A.
donc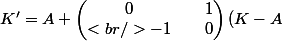)
Calcul du point B' :
jpense avoir une méthode sexy :
Pour l'angle A'B'C', c'est le même que l'angle ABC. De plus, (BB') est la bissectrice de l'angle ABC.
Donc l'idée, c'est de calculer les coordonnées de B', avec K le projeté orthogonal de B' sur (AB).
Du coup, on a un triangle rectangle BB'K rectangle en K, avec KB' = D et KBB' = ABC/2
l'angle ABC on peut se le faire easy.
et on déduit alors = \frac{KB'}{BB'} \leftrightarrow BB' = \frac{KB'}{sin(KBB')})
d'ou on déduit - B)
apres, on fait rebelotte avec C'...etc
pis pour le dernier point, ben comme point le point A'
Quand ya des lettres toutes seules ca représente un vecteur (genre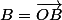 )
)
pas testé. Mais dans l'idée ca doit être pas trop bad...
rq : pour les différents points de la polyligne on peut fairemieux en fait.
Si on trouve le rapport d'homothétie entre ABCD et A'B'C'D', alors apres qqsoit les points I, J de notre polyligne, on aura
du coup, quand on a trouvé notre point B' et notre point C', on calcule le rapport
pis on pourra parcourir de proche en proche la polyligne!
mettons donc tes points A,B,C,D qui forment ta polyligne.
donc on s'interesse que à A B et C.
On va appeler A',B',C' la nouvelle polyligne.
On a (A'B')//(AB) ET (B'C')//(BC) avec d((A'B'), (AB))=d((B'C'), (BC))=e (ou d((ST),(UV)) représente la distance entre la droite (ST) et la droite (UV).
Pour le point A', en supposant qu'on a un angle du mur au bout orthogonal (donc BAA' = 90), on se place sur [AB] avec un point K.
et on écrit AK=e, pis on fait rotater le point K de -90° pour avoir notre point A'=K'.
donc les cordo de K sont données par la relation
d'ou
ensuite, on rotate K par rapport à l'origine A.
donc
Calcul du point B' :
jpense avoir une méthode sexy :
Pour l'angle A'B'C', c'est le même que l'angle ABC. De plus, (BB') est la bissectrice de l'angle ABC.
Donc l'idée, c'est de calculer les coordonnées de B', avec K le projeté orthogonal de B' sur (AB).
Du coup, on a un triangle rectangle BB'K rectangle en K, avec KB' = D et KBB' = ABC/2
l'angle ABC on peut se le faire easy.
et on déduit alors
d'ou on déduit
apres, on fait rebelotte avec C'...etc
pis pour le dernier point, ben comme point le point A'
Quand ya des lettres toutes seules ca représente un vecteur (genre
pas testé. Mais dans l'idée ca doit être pas trop bad...
rq : pour les différents points de la polyligne on peut fairemieux en fait.
Si on trouve le rapport d'homothétie entre ABCD et A'B'C'D', alors apres qqsoit les points I, J de notre polyligne, on aura
du coup, quand on a trouvé notre point B' et notre point C', on calcule le rapport
pis on pourra parcourir de proche en proche la polyligne!
la vie est une fête 
fatal_error a écrit:rq : pour les différents points de la polyligne on peut fairemieux en fait.
Si on trouve le rapport d'homothétie entre ABCD et A'B'C'D', alors apres qqsoit les points I, J de notre polyligne, on aura
du coup, quand on a trouvé notre point B' et notre point C', on calcule le rapport
pis on pourra parcourir de proche en proche la polyligne!
D'où tu sors qu'il y a une homothétie ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

