Dérivés 1ereS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
FaaLLoow
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Jan 2011, 20:41
-
 par FaaLLoow » 16 Jan 2011, 20:52
par FaaLLoow » 16 Jan 2011, 20:52
Bonjours à tous, je suis bloqué sur une question d'un exercice.
On considère la fonction f(x) = x-sinx sur [0,+°°[
1) étudier les varations de f
2)en déduire pour tout x > 0 que sinx < x
1)Pour la 1 ca le donne :
h(x) = x-sinx
Donc h'(x) = 1-cosx
Donc je cherche le signe de h'(x) pour connaitre la variation de h(x) avec le théorème de lagrange :
On sait que -1ou= 0 pour tout x
Donc h est croissante sur [0, +°°[
Donc normalement ma réponse est complète (dites moi s'il y a quelque chose à rajouter)
2) Pour la 2 je suis complétement bloqué javais une piste mais ca me parait faux :
h est croissant sur [0, +°°[ donc x-sinx >ou= 0 (ce qui je pense est faut car c'est la dérivé qui est >ou= 0) donc pour tout x>0, x>sinx
Voila si vous pourriez me donnez un petit coup de pouce il serait le bienvenu :)
Merci d'avance
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2011, 20:53
par XENSECP » 16 Jan 2011, 20:53
Le tableau de variations de h complet t'aurait aidé...
Quand je dis complet c'est avec la valeur "aux bornes" (en l'occurrence h(0)).
-
FaaLLoow
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Jan 2011, 20:41
-
 par FaaLLoow » 16 Jan 2011, 21:04
par FaaLLoow » 16 Jan 2011, 21:04
J'ai essayé mais je comprend pas trop le système car h est dérivable que sur [0, +°°[ donc le tableau de signe me parait pas trop utile car h ne varie pas et est tout le temps croissant.
Sinon ca donnerais sa je pense
x 0 +°°
f'(x) +
f 0 CROISSANT
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2011, 21:08
par XENSECP » 16 Jan 2011, 21:08
FaaLLoow a écrit:J'ai essayé mais je comprend pas trop le système car h est dérivable que sur [0, +°°[ donc le tableau de signe me parait pas trop utile car h ne varie pas et est tout le temps croissant.
Sinon ca donnerais sa je pense
x 0 +°°
f'(x) +
f 0 CROISSANT
Oui je suis d'accord que c'est inutile sauf que maintenant tu "vois" peut être mieux le signe de h ?
-
FaaLLoow
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Jan 2011, 20:41
-
 par FaaLLoow » 16 Jan 2011, 21:11
par FaaLLoow » 16 Jan 2011, 21:11
Oui c'est sur ^^. Sinon pour la question 2? parce que je comprends pas trop comment resoudre cette question par déduction.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2011, 21:13
par XENSECP » 16 Jan 2011, 21:13
FaaLLoow a écrit:Oui c'est sur ^^. Sinon pour la question 2? parce que je comprends pas trop comment resoudre cette question par déduction.
Euh j'espère que tu déconnes !
Je viens de te parler du signe de h (ou f, ça a l'air d'être la même chose) ! C'est pas pour rien...
-
FaaLLoow
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Jan 2011, 20:41
-
 par FaaLLoow » 16 Jan 2011, 21:22
par FaaLLoow » 16 Jan 2011, 21:22
D'accord donc à partir du tableau de signe au dessus, je peux en déduire que f(x) est croissant donc que x>sinx sur [0,+°°[ ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2011, 21:24
par XENSECP » 16 Jan 2011, 21:24
Le tableau de signes de f ' te donne que f est croissante... Mais avec le tableau de variations de f tu constates que f est positive sur
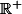
donc tu as répondu à ta question 2 ! Non ?
-
FaaLLoow
- Membre Naturel
- Messages: 10
- Enregistré le: 16 Jan 2011, 20:41
-
 par FaaLLoow » 16 Jan 2011, 21:27
par FaaLLoow » 16 Jan 2011, 21:27
Oui effectivement, je pensais ça plus compliqué j'&i plus qu'a en déduire avec le tableau que x>sinx.
Merci & bonne soirée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
