Dérivées/tangentes

[juju78]

Bonjour, j'ai un souci avec cet exo :

Soit les fonctions f et g telles que

f(x)= 3x/x+2 et g(x)=1/2x² + 3/2x

comment demontrer que les courbes Cf et Cg sont tangentes

[tigri]

bonjour

tu peux chercher s'il existe x tel que f '(x) = g'(x) ; s'il en existe, cela voudra dire qu'au point d'abscisse x les tangentes à l'une et l'autre courbe auront le même coeff directeur

[le gnome du 15]

Deux courbes sont tangentes quand elles ont un unique point d'intersection.
Pour démontrer que ces deux courbes sont tangentes, tu dois établir un système d'équation du type :
y=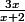
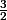y=x²+x.
et prouver qu'il n'y a qu'un seul couple de solution à ce système.

Après résolution du système, je trouve comme solution le point (0;0).

[tigri]

personnellement je ne connais pas cette définition de "courbes tangentes"

[Daragon geoffrey]

slt tt le monde, je pense que la méthode indiquée par tigri est la bonne cad de résoudre l'égalité f'(x)=g'(x) !!! @ +