Bonjour Dranaëlle,
Dranaëlle a écrit:" Trouver deux entiers positifs a et b, a est supérieur à b, tels qu'en aditionnant leur somme, leur produit et leur différence, on trouve 2005."
Donc en gros,
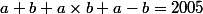
si j'ai bien saisi, mais après ?
Tu as tout à fait raison, c'est bien l'équation qu'on obtient.
Ensuite, il faut simplifier ce qu'on peut simplifier (en maths, on dit :
réduire)
L'équation devient donc

Attention, ne pas confondre
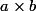
(a fois b, ou encore a multiplié par b) et
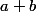
(a plus b).
Aussi, en classe de seconde, on commence à écrire le signe multiplié par

avec un point

ou même aucun signe (
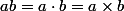
)
Revenons à notre équation

Nous avons deux inconnues, a et b, et une seule équation. En principe, on ne peut pas résoudre, car il faut autant d'équations que d'inconnues.
Sauf que là, il y a une petite astuce : on ne cherche que les solutions en nombres entiers. On peut donc utiliser l'arithmétique.
On remarque que

est facteur commun du membre de gauche. En effet, on peut
factoriser par

. On obtient,
 = 2005)
. Pourquoi c'est mieux? Parce qu'on a écrit 2005 comme le produit de deux nombres entiers. Les nombres

et

sont donc des diviseurs de 2005, et les diviseurs de 2005, on les connait, il y en a un nombre fini.
On fait les divisions successives pour les obtenir : 2005 est divisible par ?
Le quotient est-il divisible par un nombre autre que 1 ? Est-ce un nombre premier? Connais-tu le crible d'Eratosthène pour déterminer si un nombre est premier?
(Au niveau seconde, si tu sais faire cet exercice, pas grand chose ne te posera problème)
