Ineg2
Olympiades mathématiques, énigmes et défis
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 19 Juin 2010, 11:38
par windows7 » 19 Juin 2010, 11:38
salut
soient a1, .. an > 0 et a1+.. + an=1
prouvez l'inegalité suivante :
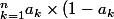 \leq \frac{(n-1)^n}{n^{2n}})

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 19 Juin 2010, 12:17
par Olympus » 19 Juin 2010, 12:17
À première vue, AM-GM plus d'autres trucs, enfin, je verrai si j'y arrive ^^

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 19 Juin 2010, 12:43
par Olympus » 19 Juin 2010, 12:43
Trouvé, que du AM-GM en effet, je posterai la preuve après avoir bouffé :we:
-
poiuytreza
- Membre Naturel
- Messages: 72
- Enregistré le: 22 Avr 2009, 13:40
-
 par poiuytreza » 19 Juin 2010, 12:44
par poiuytreza » 19 Juin 2010, 12:44
C'est sûrement pas le plus joli, mais on peut utiliser la concavité de la fonction
))

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 19 Juin 2010, 13:11
par Olympus » 19 Juin 2010, 13:11
Par AM-GM, on a :
 ( inégalité 1 )
( inégalité 1 )et
 - a_i \right) \geq n \sqrt[n]{\bigprod_{i=1}^n\left( \left( \bigsum_{j=1}^n a_j \right) - a_i \right)})
Cette dernière inégalité peut se réécrire comme :
 \left( \bigsum_{i=1}^n a_i \right) \geq n \sqrt[n]{\bigprod_{i=1}^n\left( \left( \bigsum_{j=1}^n a_j \right) - a_i \right)}) ( inégalité 2 )
( inégalité 2 ) Car
 - a_i \right) = \left( n-1 \right) \left( \bigsum_{i=1}^n a_i \right))
.
On élève à la puissance
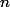
les deux membres de nos deux inégalités 1 et 2, puis on conclut .
CQFD ^^
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 19 Juin 2010, 15:06
par windows7 » 19 Juin 2010, 15:06
c'est qu'il les aime les inegalités le jeunot :++:

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 19 Juin 2010, 15:20
par Olympus » 19 Juin 2010, 15:20
Eh bien c'est à moi de proposer une inégalité maintenant ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités