Probleme sur un DM d'analyse pour vendredi 24/03/06...

[backos]

Bonjour,je suis en école d'ingenieur, j'ai absolument besoin d'aide pour ce devoir maison d'analyse, qui est plutot un DM d'algebre sur les Groupes, et toujours aucune idée. La classe lutte tout autant que moi et pas moyen de décaler la date...
Toute aide est la bienvenue, merci d'avance...

Voici le sujet:
http://aldebaran.devinci.fr/~cagnol/promotion2010/cs103/D4-cs103-05.pdf

[Alpha]

Salut, tous ces exercices sont du niveau maths sup et sont assez classiques.

Je vais répondre en partie pour le I. En fait, les sous-groupes de R,+ sont soit de la forme aZ, où a est le plus petit élément de ton ensemble A (ou l'opposé de ce plus petit élément...), soit ils sont denses dans R, ce qui prouve alors que 0 est adhérent à ce sous-groupe, donc à A.

L'idée est simple : plaçons-nous dans le cas où A admet un plus petit élément qu'on note a. Soit alors c un réel positif appartenant à G, c'est à dire un élément de A. Alors il existe un entier n tel que na< c < (n+1)a, mais zzzalors 0=< c-na < a, donc puisque a est le plus petit élément de A, c-na=0 id est c=na... Donc A est de la forme na, n appartenant à n.
Si A n'admet pas de plus petit élément, alors il est évident que 0 lui est adhérent.

Voilà,

A+

[Alpha]

Une remarque : le I et le II font double emploi, ils font démontrer la même chose.

A+

[backos]

Merci bien je vais essayer d'avancer dans cette direction.

A plus tard

[backos]

Voila les exercices 1 2 et 4 sont bouclés, mais par je ne trouve pas la deuxieme et troisieme question de l'exercice 3.

Merci de vos aides

[Alpha]

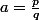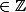Salut, si est rationnel, il s'écrit , où et sont premiers entre eux. Donc est l'ensemble des , , . On peut aussi écrire que les éléments de sont les. Et comme et sont premiers entre eux, on "sent" bien que va parcourir tout entier quand et vont parcourir !
En effet, cela se voit avec le théorème de Bezout : ce théorème dit que si et sont premiers entre eux, alors il existe et dans tels que .
Il s'ensuit alors que pour tout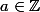 , (en multipliant l'égalité ci-dessus par ) peut s'écrire sous la forme (ici ). Donc , donc est monogène de générateur .

Cordialement, Alpha