DM(S) Trigonometrie.

[Neochrome]

Bonjour, je suis actuellement au travail sur mon devoir de mathématique.
Je ne suis pas sur des résultats que je trouve et j'aimerai si possible confirmation ou correction et explications de mes erreurs, au niveau de la méthode ou du résultat.

Actuellement j'en suis a:
A= cox(x) + cos(x+2;)/3) +cos(x+4/3)
= cos(x) + [cos(x) + cos(2;)/3)] - [sin(x) x sin(2;)/3)] + [cos(x) x cos(4;)/3)] - [sin(x) x sin(4;)/3)]
=cos(x) -( 1/2)cos(x) - [(;)3)/2]sin(x) - (1/2)cos(x) + [(;)3)/2]cos(x)
=cos(x) -( 2/2)cos(x)
A= 0

Est-ce bon? Merci ;)

J'ajouterais surement d'autre questions ou resolutions au fur et a mesure de ma progression dans ce devoir^^

[oscar]

Bonjour A = cos x +cos ( x +2pi/3) + cos(x +4pî/3
Ta réponse est bonne mais c' est long

[Neochrome]

Merci ;) Ca m'evitera de refaire les memes erreurs si erreur il y a, ou me motivera a appliquer cette fastidieuse méthode (un peu simplifiée sur le forum par rapport a la copie papier, car j'ai souhaiter détaillé le premier exemple pour que la prof puisse voir mon raisonement.) aux autres questions ^^

Edit;
Et bien, merci beaucoup ;) Aurais-tu une solution plus rapide pour simplifier l'expression ?

[oscar]

Voila ma solution
A = cos x + cos(4pi/3+x) +cos ( 2pi/3+x)
A = cosx + 2 cos (4pi/3 +x + 2pi/3 +x) /2 * cos (4pi/3 +x - 2pi/3 -x)/2
A= cos x + 2cos( 6pi/3 +2x)/2 * cos ( 2pi/3)/2
A = cos x + cos pi+x) *1/2= cosx - cosx =0
Formule utilisée cos a +cos b= 2 cos (a+b)/2 * cos (a-b)/2

Tu as bien ravaillé aussi

[Ericovitchi]

As tu appris les nombres complexes ? ou pas encore ?

Si oui imagines les 3 racines de l'équation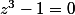
C'est 1 et
la somme des racines d'un polynôme de degré 3 c'est c'est - le coef de z² / coef de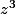 . En l'occurrence c'est donc zéro. Si on tourne le repère de x, ça ne change rien et les 3 affixes deviennent :, ,
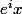La somme des 3 parties réelles de ces racines est donc nulle et donc A=0
(et la somme des 3 sinus aussi)

[Neochrome]

Merci. Si l'on prend la meme equation, en remplacant cos par sin aux trois emplacement de l'equation originale, la simplification arrive a la meme conclusion A=0.
Est-ce bon?


Edit: Ericovitchi a répondu a ma question, merci ;)
Non, je n'en suis pas encore a ce stade des chiffres complexes, mais merci, cela me servira surement par la suite.

[Neochrome]

Je suis face a une equation similaire (2pi/3 est remplacé par pi/3 , et 4pi/3 par 2pi/3), seulement, derriere les cos se trouve un²

Ca donne A'= cos²x + cos²(x+pi/3) + cos²(x+2pi/3).
Cela change-t-il quelque chose dans la methode, les formules et la facon de s'y prendre?
Je ne sais pas si je dois applique la formule en developant une fois de plus, et je ne sais pas vraiment quoi faire du².
Dois-je refaire la meme methode, en greffant simplement ² derriere chaque cos ?

[Ericovitchi]

pour démontrer la formule des sinus, un moyen élégant était de dériver l'expression en cos.

Pour A' essayes de transformer les cos² en cos par la formule cos²x=(1+cos2x)/2

[Neochrome]

Je développe comme A, laissant le ² derriere le cos, puis apres mes formules d'aditions, j'utilise la formule que tu ma donné pour redevelopper resimplifier, c'est ca?
DOnc en gros je fais A, puis une fois la, avant de réduire en effectuant les opération, j'utilise ta proprietée?

Ou j'utilise d'abord la tienne, avant d'utiliser celle utilisées en A ?

[Neochrome]

Quoi qu'il en soit je crain de me retrouver avec une formule énorme...

[Ericovitchi]

Tu pars de A'= cos²x + cos²(x+pi/3) + cos²(x+2pi/3)

Tu remplaçes les cos²x par (1+cos2x)/2
Tu retombes sur A (avec 2x à la place de x mais ça n'est pas grave puisque ce qui est vrai pour x l'est aussi pour 2x) donc la somme des 3 cosinus est nulle et il ne reste que 3/2

[Neochrome]

Nous n'avons pas encore vu les chiffres complexes tels que tu les a abordés plus tot, et je me retrouve non pas avec cos²x mais cos²(x+b) , et ca me perturbe en fait.
Je dois le faire, je crois, en utilisant les formules d'adition et de duplication seulement (puisque le chapitre porte essentiellement la dessus).
Je ne me souviens pas de proprietées sur la somme des cosinus.

Faut-il que j'applique "ta" formule en utilisant x+b de mon equation, comme etant x de la formule?

[Ericovitchi]

je ne comprends pas ce que tu dis.
je ne peux pas te dire mieux, ça prends deux lignes :
A'=cos²x + cos²(x+pi/3) + cos²(x+2pi/3)=(1+ cos 2x)/2+(1+cos2(x+pi/3))/2 + (1+cos2(x+2pi/3))/2 = 3/2 + cos 2x + cos (2x+2pi/3) + cos (2x+4pi/3)=3/2

[Neochrome]

C'est ce que je pensais, x+b = x en quelque sorte.
Merci beaucoup, je commence a comprendre la procédure ;)

J'ai ensuite la meme formule mais avec sin², quelle proprietée dois-je appliquée?
(sin x)²= [ 1-cos(2x)] /2
Ou y'a t(il plus simple?
Déja, sin²(x) est -il bien egal a [sin(x)]² ?

[Neochrome]

J'ai efectuer l'opération et me retrouve en ligne finale avec
=(1-cos2x)/2 + (1-cos2(x+pi/3))/2 + (1-cos2(x+2pi/3))/2
=(1-cos2x)/2 + (1-cos(2x+2pi/3))/2 + (1-cos(2x+4pi/3))/2

C'est bon?
Ensuite je pense que c'est egal au final 3/2, a priori, mais j'aimerais que vous m'expliquiez plus en detail comment arriver a extraire 3/2 de cette equation et finir la simplification

[Ericovitchi]

oui oui c'est ça, la somme des 3 cosinus est égale à zéro car c'est A et il reste 1/2+1/2+1/2=3/2

la somme de cos² = 3/2 la somme des sin² est aussi égale à 3/2 et d'ailleurs on est rassuré de trouver ça car cos²+sin²=1
la somme des 2 formules est donc = 3 et c'est bien 3/2 + 3/2

[Neochrome]

Mathématique, sur une copie, cela se simplifierai tout simplement par le passage de B'=(1-cos2x)/2 + (1-cos(2x+2pi/3))/2 + (1-cos(2x+4pi/3))/2
B' = 3/2

Ou pense tu que je doive ecrire les etapes intermédiaires (somme des cosinus, puis le reste ?)

[Neochrome]

Me voila arriver a la derniere question du dernier excercice obligatoire (ayant fait seul la fin du premier, les autres et le début de celui ci, mais la j'aimerais conseils).
Je dois resoudre des equations dans ]-pi;pi]
cos(x) + sin(x) = -1
cos(x) + sin(x) = racine de 2
cos(x) + sin(x) = 1/racine de 2
cos(x) - sin(x) = racine de 2

Je ne comprend pas tres tres bien la question déja au début, enfin j'ai du mal a la cernée. Je dois trouver le reel X entre -pi et pi pour qui l'equation est egal au n final, c'est ca?
Ensuite la méthoque, les echanges equivalents ne marchent pas ici je pense, je ne vois pas vraiment comme m'y prendre pour obtenir un x=n.

[dudumath]

sin²=1-cos² puis change de variable X=cos x et tu tombes sur un polynome

[Neochrome]

Erf =/ Ca ne m'avance pas du tout, etant donné que j'ai du mal a comprendre. Enfin je veux dire je sais ce qu'est un polynome, mais par exemple, je fais, pour le premier
(sinx)²= -1 -(1-cosx)²
Ensuite... je ne vois pas du tout, desolé.. :(