bonjour
je veus demontrer le lemme d'hadamard et je ne sait pas par ou commencer,
alors si quelqu'un de vous a une indication ça sera d'une qrande utilite pour moi
et merci.
voici l'ennoce du lemme:
Soit f:Rn->R une fonction de classe .
* si f(0)=0, alors il existe des fonctions g1,...,gn de classe telles que:
f(x)=somme(xi*g(x)i) i=1,.......,n
Lemme d'hadamard
2 messages
- Page 1 sur 1
Je reprends l'énoncé où il manque deux trois trucs.
Soit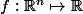 fonction de classe
fonction de classe 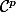 , où
, où 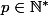 .
.
Montrer qu'il existe n fonctions) telles que :
telles que :
=\sum_{i=1}^n x_i g(x)) .
.
Et bien l'astuce est de réutiliser ce qu'on connait déjà, i.e. les fonctions réelles d'une variable réelle.
On pose=f(tx)) . Comme f est
. Comme f est 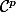 ,
, 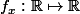 aussi par composition.
aussi par composition.
Or,=df_{tx}(x)=\sum_{i=1}^n x_i\times\frac{\partial f}{\partial x_i}(tx)) , théorème de composition des fonctions différentiables, et utilisation des dérivées partielles (cours de calcul différentiel).
, théorème de composition des fonctions différentiables, et utilisation des dérivées partielles (cours de calcul différentiel).
On a aussi la formule fondamentale de l'intégration pour les fonctions continues, ce qui est le cas ici :
=f_x(1)=f_x(1)-f_x(0)=\int_0^1 f_x'(s)dt=\sum_{i=1}^n x_i g_i(x)) , avec
, avec  =\int_0^1 \frac{\partial f}{\partial x_i}(ux)du) .
.
On vérifie bien que les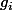 sont
sont 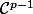 .
.
Soit
Montrer qu'il existe n fonctions
Et bien l'astuce est de réutiliser ce qu'on connait déjà, i.e. les fonctions réelles d'une variable réelle.
On pose
Or,
On a aussi la formule fondamentale de l'intégration pour les fonctions continues, ce qui est le cas ici :
On vérifie bien que les
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
