Probleme concernant la section d'un cube

[camilletro]

Bonjour, je travaille depuis des heures sur un exercice de géométrie dont je n'arrive pas a résoudre.
Je me perme de vous le proposer :
Dans un cube ABCDEFGH d'arrete 5, on trace [AG] et on coupe ce cube par un plan orthogonal à cette diagonale en un point M situé à une distance d de A.
on admet que (AG)est orthogonale à (CFH) et à (DBE) et que les vecteurs : AD+AB+AE=AG
- demontrer que (AG)perce (DBE) en un point M qui est le centre de gravité de DEB et préciser sa position sur (AG) (j'ai essayer de résoudre avec les barycentres mais sans grand résultat)
- determiner l'intersection de (AG) avec (CFH)
-etudier la nature de la section suivant d

on note A l'aire de la section Q
- pourquoi le maximum et le minimum de A est atteint pour des reels d de l'intervalle [5racine carré de 3/3 ; 10 racine carré de 3/3 ]

pouvez vous me doner des pistes de réflexions... merci d'avance et très bonne journée

[Huppasacee]

Bonjour

Il est donc admis que AG est perpendiculaire au plan DBE

et soit M l'intersection de AG et de ce plan DBE

Alors le produit scalaire de tout vecteur de ce plan avec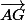 est nul

Donc le produit scalaire

= 0

décomposer les vecteur MD, MB et ME en passant par A

et utiliser :

AD+AB+AE=AG

pour montrer que la somme des vecteurs


est nécessairement nulle et on trouvera par la même occasion la norme de AM ( vecteur